定期テストも入試も怖くない!数学の証明問題をラクにとくための定期&入試攻略法

「証明問題」と聞くと、なんだか難しそう…そう感じる人は多いのではないでしょうか。
数学の中でも証明問題は、
- 「考え方はわかっているのに、どう書けばいいかわからない」
- 「途中で詰まってしまう」
という声がよく聞かれる単元です。特に定期テストや入試では、“考え方”だけでなく、“書き方”ができていないと点数にならないため、苦手意識を持つ生徒が少なくありません。

しかし、実は証明問題は「書き方の型」さえ身につければ、誰でも得点源にできる分野なのです。
文章の流れや使う言葉には一定のルールがあり、それを理解すれば、証明は「センス」ではなく「手順」で解けるようになります。
つまり、
- 1)「型を覚える」
- 2)「自分の言葉で書けるようにする」
- 3)「練習して定着させる」
という3ステップで、着実に得点アップが狙えるのです。
また、近年の入試傾向を見ても、思考力や表現力を問う「証明型問題」は年々増えています。
たとえば大阪府の高校入試問題では、
- 「図形の性質を利用して説明しなさい」
- 「ある条件を満たすとき、~が成り立つことを証明せよ」
といった出題が多く見られます。これらは一見難しそうに見えても、「仮定→結論→理由」という基本の流れを守ることで、確実に書き進めることができます。
このコラムでは、証明問題を苦手から得意に変えるために必要な「考え方」と「書き方」の両面を、6章に分けてわかりやすく解説していきます。
まずは、証明が苦手になる原因を理解し、次に「型」をつかみ、そして「実際の書き方」をマスターしていきましょう。定期テスト対策から入試の実戦まで、すぐに使えるテンプレートやコツも紹介します。
読み終わるころには、「証明って意外とカンタンかも」と感じられるはずです。
目次
第1章:証明問題が苦手な理由は“書き方”にある!
「証明問題が苦手」と感じる生徒の多くが口をそろえて言うのが、
「考え方はわかるけど、どう書けばいいかわからない」
という言葉です。図形の性質や定理を理解していても、答案の“文章”にする段階で止まってしまう。
つまり、証明が難しいのではなく、「書き方の型」を知らないことこそが苦手の原因なのです。
証明問題は“数学の作文”。文章の構成ルールや書き方を知れば、むずかしい理屈を使わなくても、スムーズに書けるようになります。
この章では、証明が苦手になる3つの原因と、その克服の第一歩を整理してみましょう。

「何から書けばいいのかわからない」
多くの生徒が最初につまずくのが、「書き始め方」。
問題文を読んでも、「最初に何を書くべきか」がわからず、手が止まってしまうのです。
実は証明には、“お決まりの書き出し”があります。
それが「△ABCと△DEFにおいて」や「仮定より」「与えられた条件から」などの定型フレーズです。書き始めを決めておくことで、スタート時の迷いがなくなります。
「筋道はわかっても文章化できない」
次の壁は、「頭の中では理解できているのに、それを文章にできない」というケースです。
たとえば「二つの三角形の辺の長さが等しいから合同になる」と思っても、答案では「対応する3組の辺がそれぞれ等しいから、三角形は合同である」と書かないと点がもらえません。
つまり、数学的に正しい言葉で説明する力が求められます。これは“考える力”ではなく、“書く練習”で身につく力。ワークや解答例を参考にして、「理由の書き方」「つなぎ言葉の使い方」を真似ることが、得点アップの近道です。
「書き方に一貫性がない」
最後の原因は、「書くたびに表現がバラバラになる」こと。
文末が「~である」「~です」で混ざったり、式や記号の使い方が統一されていなかったりすると、採点者に“雑な印象”を与えてしまいます。
証明は「正しいことを、わかりやすく伝える」問題。内容が合っていても、書き方に一貫性がないと減点されることもあります。
そこで大切なのが、自分なりの書き方ルールを持つこと。
たとえば、
- 「文末はすべて『~である』にする」
- 「根拠を書くときは必ず“なぜなら”を入れる」など、
書くルールを決めておけば、安定した得点が狙えます。

証明問題が苦手になる理由は、「考え方」よりも「書き方」にあります。
- 文章の始め方
- 理由の伝え方
- 文の統一感
――この3点を意識するだけで、証明問題は一気に「わかる」から「書ける」へと変わります。
次の章では、証明の基礎である「仮定→結論→理由」という流れを使って、どんな問題でも迷わず書ける“証明の型”を身につけていきましょう。
第2章:証明の基本構造をつかもう
「仮定→結論→理由」の流れ
証明問題をスラスラ書ける人は、実は特別なひらめきや才能があるわけではありません。彼らが共通して持っているのは、「文章の型(=証明の流れ)」を理解していること。
証明にはどんな問題にも通じる基本構造があり、それが
「仮定 → 結論 → 理由」 の3ステップです。
この章では、証明の流れを図解で整理しながら、「何から書いて、どうつなげればいいのか」が一目でわかるように解説します。この型をマスターすれば、どんな証明問題も「手順通りに書くだけ」で形になるようになります。
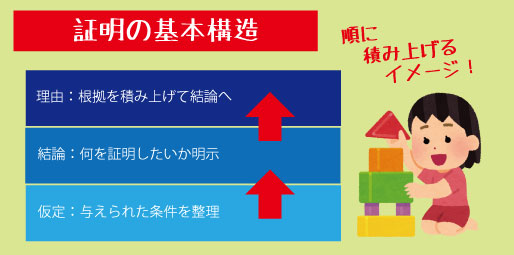
「仮定」― 問題文の中から“出発点”をつかむ
証明のスタートは、与えられた条件を整理することから始まります。
この部分が「仮定」です。問題文に書かれている「~である」「~とする」という部分を、まずは抜き出して書きましょう。
たとえば、
- 「△ABCは二等辺三角形で、AB=ACである」
- という条件が与えられているなら、最初に書くべきは
- 「△ABCにおいて、AB=ACである。」
です。
ポイントは、問題文の言葉をそのまま使うこと。無理に言い換えようとせず、まずは“仮定を正確にうつす”ことから始めるとミスが減ります。
「結論」― 何を証明すべきかをハッキリさせる
次に書くのが「結論」です。ここでは、「何を示したいのか」をはっきり言葉にします。
たとえば、
- 問題文に「∠B=∠Cを証明せよ」とあれば、
- 「∠B=∠Cであることを証明する。」
- という一文を最初の段落に入れるのが基本です。
意外と多いのが、「結論部分を書き忘れる」ミス。採点する先生にとって、どこを証明したいのかが明確でないと減点対象になります。証明文の冒頭に“結論宣言”を置くことで、文章全体がぐっと読みやすくなります。
「理由」― 根拠を順に積み上げる
証明の本体は「理由」です。仮定から結論を導くために、「なぜそう言えるのか」を筋道立てて書いていきます。
たとえば、
- 「AB=AC」から「∠B=∠C」を導く場合、
- 「AB=ACだから、二等辺三角形の性質より、∠B=∠Cである。」
と書くように、根拠+結果のセットで書くのがコツです。
「なぜそうなるか」を説明する部分を飛ばしてしまうと、“結果だけ並べただけの文章”になってしまい、点数が伸びません。理由を書く際は、定理名や性質をきちんと書く意識を持ちましょう。
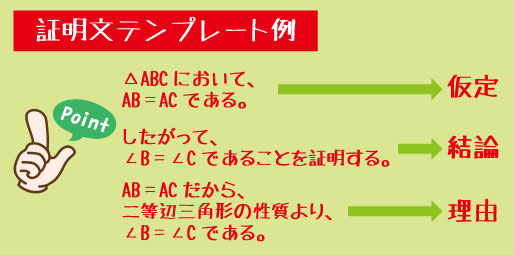
証明の流れは、どんな問題でも共通しています。
「仮定 → 結論 → 理由」
この順番を意識して書くだけで、証明文の“形”が自然と整います。最初はテンプレートのように使って構いません。「仮定をうつす → 結論を宣言 → 理由を積み上げる」この流れを何度も練習するうちに、自分の言葉でスラスラ書けるようになります。
次の章では、この構造を活かして、定期テストや入試でよく出る「合同」「相似」「平行」などの定番証明パターンを具体例で見ていきましょう。
第3章:よく出る証明パターン3選
図形問題を中心に
証明問題には、どんな学校・入試でも必ず登場する「定番パターン」があります。特に図形分野では、合同・相似・角度・平行などが毎年のように出題されます。一見内容が違うように見えても、実は“使う型”はほぼ共通。
この章では、定期テストから高校入試までで最もよく出る3つのパターンを取り上げ、それぞれの
- 「狙われやすい書き方」
- 「使えるフレーズ」
- 「よくあるミス」
までを整理していきます。ここを押さえておけば、証明問題は“暗記で乗り切れる単元”に変わります。
パターン①「合同の証明」
3つの対応関係をそろえる!
最も基本であり、最も出題頻度が高いのが合同の証明です。
合同とは「形と大きさがまったく同じ」ということ。これを証明するには、次の5つの条件のうちどれか1つを満たせばOKです。
- ① 3組の辺がそれぞれ等しい
- ② 2組の辺とその間の角がそれぞれ等しい
- ③ 1組の辺とその両端の角がそれぞれ等しい
- ④ 直角三角形で斜辺と1つの鋭角がそれぞれ等しい
- ⑤ 直角三角形で斜辺と他の一辺がそれぞれ等しい
【例文】
- △ABCと△DEFにおいて、AB=DE、AC=DF、∠A=∠Dである。
- よって、2組の辺とその間の角がそれぞれ等しいので、
- △ABC≡△DEFである。
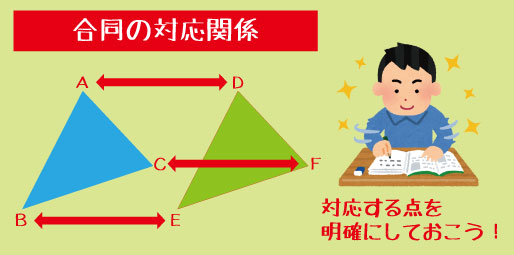
💡コツ
「対応する」関係を明確にするため、図中にA↔Dなどの対応点を矢印で書き込む練習をしておくと◎
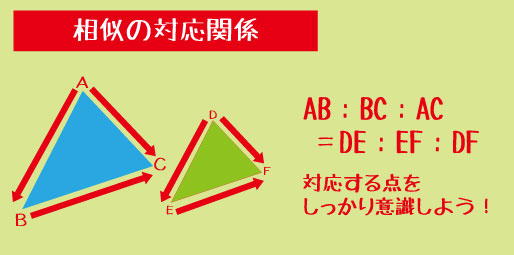
パターン②「相似の証明」
比と角度の関係を整理せよ
2つ目は相似の証明。合同と似ていますが、ポイントは「形が同じで、大きさが違う」こと。
次の3条件のいずれかを示せればOKです。
- ① 3組の辺の比がすべて等しい
- ② 2組の辺の比が等しく、その間の角が等しい
- ③ 2組の角がそれぞれ等しい(AA)
【例文】
- △ABCと△DEFにおいて、∠A=∠D、∠B=∠Eである。
- よって、2組の角がそれぞれ等しいので、
- △ABC∽△DEFである。
💡コツ:
辺の比を書くときは「同じ順番の対応点」を意識する。
(例:AB/DE=AC/DF)この順番がずれると、正しく相似を示せないので注意。
パターン③「平行・垂直・角度の証明」
補助線を味方に!
3つ目は「線の関係」を問う証明です。「平行であることを証明せよ」「垂直であることを示せ」などの形でよく出ます。
ここでは角度の等しさや三角形の性質を活用します。
【例文】
- 直線ABとCDについて、
- 同位角が等しい(∠1=∠2)ので、
- 直線AB∥CDである。
また、「垂直」を証明する場合は、
- ∠1=∠2=90°だから、
- AB⊥CDである。
のように90°を明記するのがポイント。
💡コツ
補助線を引く問題では、「何を示したいか」→「そのためにどんな線を引けば角度や辺が対応するか」を先に考える。
合同・相似・角度の証明は、すべて「対応関係」「理由」「結論」の3要素で成り立っています。つまり、第2章で学んだ「仮定→結論→理由」の流れを、それぞれのパターンに当てはめるだけで、どんな問題にも対応できるのです。
証明問題を練習するときは、問題を解くだけでなく「これはどのパターン?」と分類する意識を持つこと。そうすれば、“見た瞬間に書ける証明”がどんどん増えていきます。
第4章:得点を伸ばす“書き方のコツ”5選
証明問題が苦手な生徒の多くは、「考え方は合っているのに、点数が伸びない」という悩みを抱えています。その原因はずばり、「書き方のルール」や「採点者に伝わる文章の構成」を意識できていないことです。
実は、証明の内容そのものよりも、
- 「どのように表現するか」
- 「どのように順序をつけるか」
で点数が大きく変わります。
ここでは、定期テストや入試で得点を伸ばすために絶対押さえておきたい“書き方のコツ”を5つ紹介します。
最初に「仮定」「結論」をはっきり書く
証明文は、
- 「何を示したいのか」
- 「どの条件を使うのか」
が明確でないと、読み手(採点者)に伝わりません。
まずは最初に「△ABCで、AB=AC(仮定)」や「∠ABC=∠ACBを証明する(結論)」のように、文頭で宣言しましょう。
こうすることで、読み手が「この証明では何をゴールにしているのか」をすぐに理解できます。また、答案に一貫性が生まれ、減点のリスクを大幅に減らせます。
「理由」を後回しにしない
証明の途中で、「なぜそう言えるのか」を省略してしまうケースがよくあります。
しかし採点では、「理由」が書かれていないだけで減点対象になることも。
「平行だから錯角が等しい」「二等辺三角形だから底角が等しい」など、使った性質を必ず明記する習慣をつけましょう。
「→理由:~~」のように書くと、読みやすさもアップします。
段落を分けて“見やすく”
文章が詰まっていると、どこで話が変わったのかがわかりにくくなります。
証明では「仮定」「考察」「結論」など、意味が切り替わるところで段落を分けるのがおすすめ。
黒板の板書でも、先生が少し空白をあけながら書きますよね。
見た目の整理ができると、採点者にも丁寧さが伝わり、印象点にもつながります。
図に書き込みながら進める
文章だけでなく、図を使って補助線・対応角・合同条件などを書き込むと、理解が一気に深まります。
入試でも「図に情報を追加しながら考える」習慣がある生徒ほど、安定して高得点を取ります。
ただし、試験では清書用答案にごちゃごちゃと描き込まないよう注意。下書き段階で整理→清書で必要最低限を図に残すのがコツです。
結論は「~である」ではなく「よって、~が成り立つ」
最後の締めくくりは、ただ「等しい」で終わらせず、
- 「よって△ABC≡△DEFである」
- 「よって∠A=∠Dが成り立つ」
と書くことで、論理がスッキリまとまります。
文章全体が“数学的な流れ”になり、読み手に「この生徒は論理を理解している」と伝わります。

証明は「正しい内容」を書くだけでは不十分です。
- 「読みやすさ」
- 「伝わりやすさ」
- 「論理の順序」
が得点を左右します。今回紹介した5つのコツを意識するだけで、あなたの答案はぐっと“採点者目線”に近づきます。
定期テストでも入試でも、「丁寧に書ける生徒=得点が安定する生徒」。今日から、自分の証明文を見直してみましょう。
第5章:定期テスト対策
学校で出やすい証明問題の攻略法
定期テストでの証明問題は、「出題のされ方」がある程度パターン化されています。
つまり、闇雲に問題集を解くよりも、「学校テストでよく出る型」を理解し、それに合わせた練習をすれば効率よく得点できます。多くの生徒が「わかっているのに点が取れない」と感じるのは、出題形式に慣れていないから。
この章では、学校テストで頻出の証明パターンと、それぞれの攻略法を紹介します。「何を問われやすいか」を先に知ることが、点数アップの最短ルートです。
二等辺三角形の底角の証明
定期テストで最も多いのが、「二等辺三角形に関する証明」です。
たとえば、
「AB=ACのとき、∠ABC=∠ACBを証明せよ」
という問題。ポイントは、三角形の合同条件を利用して、角の等しさを導く流れにあります。
攻略のコツは次の3ステップ
- 1️⃣ 二等辺であることを仮定に書く。
- 2️⃣ その情報から使える合同条件を考える。
- 3️⃣ 合同から角の等しさを結論づける。
「合同条件→対応する角が等しい」のパターンを体に覚えさせておきましょう。
平行線を使った角度の証明
次に頻出なのが、平行線を使った角度の等しさを示す問題です。
「AB∥CDのとき、∠ABC=∠CDAを証明せよ」
といった形で出題されます。このタイプでは「錯角」「同位角」「対頂角」という3つの角の関係がカギ。
攻略ポイントは、どの角がどの角と関係しているかを図で明確にすることです。図をきれいに描いて、対応する角に印をつけるだけでも理解が進みます。
さらに、「平行線だから錯角が等しい」という“理由”を文中にしっかり書けば減点されません。
中点・線分の長さに関する証明
三角形の辺の中点を結んだ線分や、線分比を扱う証明も定番です。
たとえば、
「D、Eはそれぞれ辺AB、ACの中点である。DE∥BCを証明せよ」
という問題。この場合は、「中点連結定理」を使って
- AD=DB、AE=ECより、△ADE∽△ABC
- というように、相似の関係を利用して平行を導く流れになります。
攻略のコツは、条件(中点など)を整理して、相似条件につなげる意識を持つこと。図を活用しながら、補助線を入れて考えるとミスが減ります。
台形や長方形など特別な図形
特別な図形を使った証明もよく出ます。
「台形の上底・下底の延長線を使って角の関係を証明する」
など、一見複雑に見えるけれど、平行や合同を使う基本形に還元できることが多いです。こうした問題は、図を整理して“見えない平行・等しい角”を見つけ出す力が問われます。
難しそうな図形でも、合同・相似・平行のどれかに変換できれば、一気に解決できます。
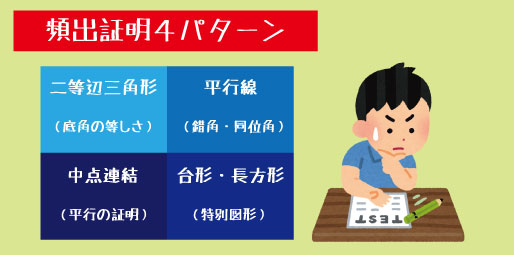
定期テストの証明問題は、「二等辺三角形」「平行線」「中点連結」「特別な図形」の4大パターンを押さえておけば安心です。学校の先生は授業で扱った内容をベースに出題するため、授業ノートに出てきた図形や定理を復習することが最高のテスト対策になります。
また、過去のテストを見返して「どんなタイプが出たか」を確認することも重要。出題傾向を知ることで、ムダな勉強を減らし、効率的に得点アップが狙えます。
第6章:入試で差がつく!
思考力型証明へのステップアップ
入試の証明問題は、定期テストのように「型」だけでは解けません。
なぜなら、入試では「与えられた条件から自分で考えて導く力(思考力)」が問われるからです。同じ証明でも、条件がひとつ足りなかったり、補助線を自分で引かなければいけなかったり…。
つまり、“考えながら作る証明”へと進化しているのです。
本章では、入試でよく出る「思考力型証明」の特徴と、それに対応できる学習ステップを紹介します。定期テストでは満点を取れても、入試で苦戦する生徒は少なくありません。ここでしっかり「入試仕様の考え方」を身につけましょう。
補助線を“戦略的に”使う練習
入試証明では、「補助線を引かないと証明が進まない」問題が多く出題されます。
補助線は“思いつき”ではなく、“目的に合わせて引く”のがポイントです。
たとえば、
- 「角の等しさを示したいなら、対頂角や錯角が現れる線を」
- 「辺の等しさを示したいなら、合同や中点を利用する線を」
といったように、目的から逆算して考えることが大切です。
練習法としておすすめなのは、問題を見て「どこに補助線を引けばよさそうか」を考えるだけのトレーニング。
実際に引かなくても、頭の中で「こう引けば平行ができる」「この線を延長すれば合同が見える」とイメージできるようになります。
論理のつながりを意識して書く
入試の証明では、「どうしてそうなるのか」を筋道立てて説明する力が求められます。
- 「AB=AC(仮定)」
- →「△ABCは二等辺三角形」
- →「∠B=∠C(結論)」
このように、一つひとつの文を矢印でつなぐイメージで書くと、論理の流れが明確になります。
また、文章の中に「なぜなら」「したがって」「よって」といった接続語を使うことで、思考の流れが自然に伝わります。特に入試では、途中式の書き方・言葉のつながり・推論の丁寧さが大きく採点に影響します。単に正解にたどりつくだけでなく、“読みやすく納得できる証明文”を書く練習をしましょう。
過去問で「出題意図」を読む
最後に、思考力型証明に慣れるための最も効果的な方法が「過去問演習」です。
過去問をただ解くだけでなく、
- 「なぜこの条件を与えたのか?」
- 「何を導かせたいのか?」
を考えることが重要です。出題者の意図を読むことで、条件の使い方や補助線の引き方が見えてきます。
特に、公立高校入試では年によって出題のテーマが少しずつ変わる傾向があるため、近年3年分を分析するのがおすすめです。「合同型」「相似型」「平行型」など、自分が苦手なパターンを把握しておくと、学習計画も立てやすくなります。

入試の証明問題は、“自分で考える力”がカギです。そのためには、
- ①条件整理
- ②補助線の使い方
- ③論理の流れ
- ④過去問分析
の4ステップを繰り返し鍛えましょう。最初は時間がかかっても、「なぜこの線を引くのか」「なぜこの条件を使うのか」を意識して練習すれば、確実に成長します。
証明のゴールは「正解を書くこと」ではなく、「論理的に説明できること」。思考力型証明を通じて、数学の本当の面白さを感じてみてください。
まとめ
証明がわかると、数学がもっと面白くなる!
数学の証明は、多くの生徒が「苦手」と感じる分野です。
しかし実際のところ、証明問題は決して特別な才能が必要なものではありません。これまでの章で見てきたように、定期テストでも入試でも、「書き方の型」と「考え方の筋道」を押さえれば、確実に点を取ることができる分野です。
第1章では、証明が苦手になる原因が「考え方」ではなく「書き方」にあることを確認しました。
そして第2章で、証明の基本構造「仮定→結論→理由」という流れを理解することで、どんな問題でも整理して書けるようになります。
第3章・第4章では、よく出るパターンや得点を伸ばす書き方のコツを紹介しました。これらを意識して練習するだけで、テストの得点は確実に上がります。
さらに第5章では、学校テストで出やすい典型問題の攻略法を、第6章では、入試で問われる“思考力型証明”へのステップアップを紹介しました。入試で問われるのは、「知っている」よりも「考えられる」力。そのためには、日々の授業やテスト勉強の中で、「どうしてそう言えるのか?」を自分の言葉で説明する習慣を身につけることが大切です。
証明の勉強は、最初は時間がかかるかもしれません。でも、コツコツと練習を重ねるうちに、「論理のつながり」が見えるようになり、数学が一段と楽しくなります。そして、自分の考えを筋道立てて説明できる力は、入試だけでなく社会に出てからも必ず役に立つ力です。
どんなに難しそうに見える問題でも、最初の一歩は「仮定と結論を整理すること」。そこから一つずつ理由を積み重ねていけば、必ず「わかった!」という瞬間がやってきます。証明問題は、解けたときの達成感が大きい分野です。焦らず、あきらめず、自分のペースで練習を重ねていきましょう。
あなたの努力は、必ず結果につながります。
このコラムで紹介したポイントを意識して、
次の定期テスト・そして入試本番で
「自信を持って書ける証明」を目指してください。
“わかる”を“できる”に変えるその一歩を、
今日から踏み出しましょう。
お子さまの学習にお悩みの保護者の方へ。

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ!!
こちら各種SNSでも情報配信中です。参考にしてみてください。
/
この記事は 2,783人 に閲覧されています。
.jpg)




条件整理のスピードと正確さを鍛える
入試証明の第一歩は、与えられた条件を正しく整理することです。
「A=B」「角C=角D」「線分が平行」など、条件をそのままノートに書き写すのではなく、図に矢印・印・記号を使って可視化しましょう。
入試問題では条件が複数混ざっていることが多く、「どの条件を使えばよいか」を見抜く力が得点を分けます。
たとえば「AB=AC」「∠ABD=∠ACD」「BD=CD」と3つ条件があったら、どれが合同の手がかりかを判断する練習を繰り返しましょう。そのためには、1問ごとに「使った条件」を声に出して確認する習慣が効果的です。