【中2数学】超簡単!連立方程式の解き方をわかりやすく解説

目次
はじめに

連立方程式は中学数学の重要な単元の一つであり、
定期テストや高校入試でも頻出のテーマです。
しかし、「解き方がわからない」「計算が合わなくて途中で投げ出してしまう」
という悩みを持つ生徒も多いのではないでしょうか?
連立方程式とは?
連立方程式とは、2つ以上の方程式を同時に満たす解(値)を求める問題のことです。一般的に中学では、以下のような2元1次方程式を扱います。
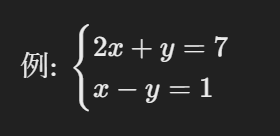
この場合、xと y の2つの変数(未知数)の値を
同時に求める必要があります。
なぜ連立方程式を学ぶのか?

・定期テストや入試で高頻出。
・実生活の問題解決に応用可能。
・数学全般の基礎力を養う上で重要。
超簡単!連立方程式の2つの解き方
連立方程式には主に代入法と加減法という2つの解法があります。
それぞれの方法を具体例を使って解説します。
1. 代入法
- 1つの式から x または y を求める。
- 求めた値をもう1つの式に代入する。
- 1つの変数を求めたら、その値を使ってもう1つの変数を求める。
例題:代入法で解いてみよう!
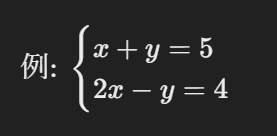
1.x+y=5 より、 y=5-x
2.y=5-x を 2x-y=4 に代入すると、 2x-(5-x)=4
展開すると → 2x-5+x-4 → 3x=9 → x=3
3.x=3 を y=5-xに代入すると、 y=5-3 → y=2
答え:x=3、y=2
2. 加減法
- 2つの式を足したり引いたりして、1つの変数を消す。
- 残った1つの変数を求める。
- 求めた値を使って、もう1つの変数を求める。
例題:加減法で解いてみよう!
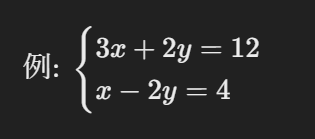
1.2つの式を足すと、
(3x+2y)+(x-2y)=12+4 → 3x+x=16 → 4x=16 → x=4
2.x=4 を x-2y=4 に代入すると、
4-2y=4 → -2y=0 → y=0
3.x=3 を y=5-xに代入すると、 y=5-3 → y=2
答え:x=4、y=0
どちらの方法を使うべき?

代入法は、式のどちらかが単純な場合に便利です
(例:y=2x+1y = 2x + 1 のような形)。
加減法は、2つの式が整理されていて、
足したり引いたりしやすい場合に向いています。
自分が解きやすい方を選ぶか、問題に応じて使い分けるのがコツです。
よくあるミスとその防止策
1. 計算ミス
・数字の符号や計算過程を確認するクセをつけましょう。
・解答を書き終えたら必ず再計算する。
2. 式を代入する際のミス
・ を代入する場合、式全体を括弧で囲んでミスを防ぎましょう。
例)y=2x+1 を y=2(3)+1 のように書く。
3. 解答を見直さない
・問題に戻り、求めた x,yを元の式に代入して確認しましょう。
練習問題で実力アップ!
以下の問題に挑戦してみましょう。
練習問題1:代入法を使って解いてみましょう。
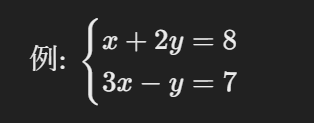
練習問題2:加減法を使って解いてみましょう。
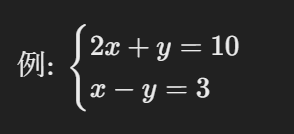
連立方程式を得意にするための勉強法
- 基礎を固める 計算力を向上させるために、簡単な計算問題を繰り返し練習しましょう。
- 問題をたくさん解く 教科書や問題集で多くの問題に触れることが重要です。
- 間違えた問題をノートにまとめる 間違えた理由を明確にし、次に同じミスをしないようにしましょう。

まとめ

連立方程式は、正しい手順を身につければ決して難しくありません。
代入法と加減法の2つの方法を使い分け、
練習問題に繰り返し挑戦することで、
得意分野に変えることができます。
- 代入法:式がシンプルな場合に活用。
- 加減法:式が整理されている場合に有効。
定期テストや高校入試での得点アップを目指し、まずは基本をしっかり押さえましょう!
個別指導で数学の苦手を克服!

連立方程式が苦手な生徒の多くは、
「どこでつまずいているのか」が明確になっていません。
個別指導塾では、
一人ひとりに合った指導で、苦手分野を徹底サポートします。
解法の基礎から応用まで指導
定期テスト&入試対策に特化
効果的な学習プランを提案
無料体験授業で、数学が得意になるきっかけをつかみましょう!
イマナビでは随時、個別の学習相談会を実施しています。
「自分に合った勉強法を相談したい」など、あなたの悩みをお聞かせください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ!!
ーーーーーーーーーーーーーーーー
こちら各種SNSでも
情報配信中です。
参考にしてみてください。
ーーーーーーーーーーーーーーーー
/
この記事は 2,343人 に閲覧されています。
.jpg)



