平方完成で差がつく！

定期テストも入試も得点アップを目指そう

数学が得意な人と苦手な人、その差が大きく出やすいのが「二次方程式」です。そして、その中でも特に理解のカギとなるのが「平方完成」の単元です。この平方完成、定期テストでも入試でも頻出の重要テーマでありながら、多くの中学生が「よくわからない」「計算が複雑でミスしがち」と感じている分野でもあります。

しかし、実は平方完成の考え方はとても論理的で、しっかりと手順を覚えて反復練習すれば、確実に身につく内容でもあるのです。また、平方完成が理解できれば、グラフの頂点を求める、解の公式を導くなど、他の単元の理解もグッと深まります。

この記事では、中学生が「平方完成」を効率よくマスターできるよう、６つのステップで丁寧に解説していきます。まずは基本の考え方と公式から始め、定期テストでの出題パターン、ミスを減らす工夫、さらには応用問題へのアプローチ方法まで幅広くカバーしています。

数学が苦手な人も、今回のコラムを通じて「意外とわかりやすい！」「できそう！」と感じてもらえるはずです。

定期テストや入試に向けて、今からしっかりと準備していきましょう！

 

 

 

 

 

第1章｜平方完成とは？

その意味と必要性を理解しよう

 

▼　実は簡単！平方完成のステップ

平方完成は一見難しそうに見えますが、実はステップを押さえれば簡単です。

• STEP１）x² + bx + c の形に整理
• STEP２）bの半分を求めて二乗する（＝b/2）²
• STEP３）足した分だけ引く※調整
• STEP４）平方の形にまとめる

たとえば、x² + 4x + 1の場合：

• b = 4 → 4/2 = 2 → 2² = 4
• x² + 4x + 1 = x² + 4x + 4 – 3 = (x + 2)² – 3

このように、ルールに沿って操作するだけで、平方の形に変換できます。はじめは混乱するかもしれませんが、練習を積めば誰でも確実にできるようになります。

▼　なぜ入試にも重要なのか？

高校入試では、関数のグラフや応用問題などで平方完成が問われることが多く、特に二次関数の頂点を求める場面で欠かせません。また、高校数学の数学Ⅰでもこのスキルが引き続き必要になります。今のうちに理解しておけば、高校数学でも大きなアドバンテージになります。

平方完成は数学力アップの第一歩！

 

第2章｜平方完成のしくみ

図と式でマスターしよう

たとえば、x² + 6x を平方完成するとき、x² は正方形（1辺がxの正方形）、6xは縦がx、横が6の長方形をイメージできます。この6xを「x×3」と「x×3」の2つに分けて、正方形の2辺にそれぞれくっつけると、「(x + 3)²」が完成し、残った角の部分（面積9）を引く必要がある、という仕組みです。

 

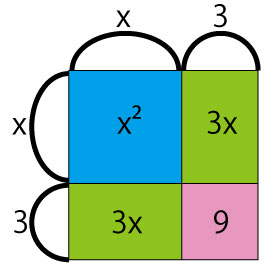
つまり、

x² + 6x = (x + 3)² – 9

という変形は、図形的にも筋が通っているのです。

▼　「完成」とは何が「完成」するのか？

「平方完成」という言葉の意味を改めて考えると、「平方（＝2乗）の形に式を完成させる」ことを指します。これは、x² + bx のような式を (x + a)² + b のように、2乗の形に変えることで、数式の構造が見えやすくなり、次のステップ（解の公式、因数分解、グラフ）に進みやすくなります。

さらに、平方完成は「関数の変換」や「グラフの頂点を求める」ことにも直結します。関数 y = x² + 6x + 5 は、平方完成により y = (x + 3)² – 4 と変形でき、頂点が (−3, −4) だとすぐに分かります。

▼　教科書ではわかりにくい？補助線と色分けで克服

教科書だけでは分かりづらい場合、図形的な補助線を使ったり、bの半分を色分けして視覚的に区別したりすると、仕組みが見えやすくなります。特にノートに書くときは、次の3つを意識すると理解が深まります。

こうした手順と補助的な工夫で、平方完成はグッとわかりやすくなります。

式の「構造」が見えると数学が面白くなる！

第3章｜実践！

平方完成で二次方程式を解こう

▼　実例で確認！平方完成の手順

では、実際に平方完成を使って二次方程式を解いてみましょう。

このように、平方完成を用いれば計算のステップはやや多いものの、公式の理解やミスの少ない計算につながります。

▼　応用力アップ！因数分解できない式にも対応

次のような因数分解できない式にも、平方完成は強力です。

このように、平方完成によって無理数が含まれる解も正確に求めることができます。これは解の公式を使った計算とも同じですが、式の構造理解という点で優れているのが平方完成です。

解の本質を理解するための一歩

第4章｜平方完成とグラフ

関係性を理解しよう

中学数学では、関数のグラフを「見える形」で理解することが求められますが、平方完成を使うことで、式からグラフの特徴が一目でわかるようになります。

▼　頂点の座標が分かれば関数がもっと得意に！

平方完成の大きな利点のひとつが、頂点の座標が簡単に求められることです。放物線のグラフを描くとき、頂点は最も重要なポイントです。

また、xの係数の符号や値によって、グラフの開き方や左右の移動も読み取れます。たとえば、

・y = (x − 2)² → 頂点は (2, 0)（y = x²を右に2移動）
・y = (x + 1)² + 3 → 頂点は (−1, 3)（y = x²左に1、上に3移動）

このように、グラフの形を頭の中でイメージできるようになると、関数の単元で圧倒的に有利になります。

▼　実力アップ！応用問題にも対応しやすくなる

高校入試や定期テストでは、グラフと式の両方を使った応用問題がよく出題されます。たとえば「頂点が○○にある放物線の式を求めなさい」や「グラフとx軸の交点の座標を求めなさい」といった問題です。

このような問題に強くなるためには、平方完成による式変形をしっかり理解しておくことが欠かせません。特に、式とグラフの関係を「見える化」する力は、今後の数学学習においても非常に役立ちます。

式とグラフのつながりを楽しもう

第5章｜得点アップのために

よくある間違いとその対処法

▼　間違いノートで「ミスの傾向」を見抜く

ミスを減らすためには、自分がどのパターンでつまずきやすいのかを分析することが重要です。「間違いノート」を作って、どこでミスをしたか、どう直すべきだったかを記録しておくと、同じミスを繰り返す確率が大きく下がります。

正しい理解と丁寧な見直しが成功のカギ

第6章：チャレンジ！！

平方完成の応用問題に挑戦しよう

▼　１）グラフと平方完成

「y=ax²+bx+cを平方完成せよ」という問題は頻出ですが、これが「グラフの頂点を求めなさい」「グラフがx軸と交わる条件を考えなさい」と変化するだけで、応用問題になります。平方完成を使って式を「頂点の形（y=a(x−p)²+q）」に変形できれば、頂点の座標(p,q)が一目でわかるようになります。

たとえば、

• y=x²+4x+5　を平方完成すると、
• y=(x+2)²+1　となり、
• 頂点は (−2,1)であることが分かります。

▼　２）解の個数と平方完成

平方完成は、解の個数を判断する場面でも活躍します。たとえば次のような問題です。

• 平方完成すると、x²−6x+k=(x−3)²−9+k=0
• ⇒　(x−3)²=9−k
• ここで、右辺が負の数になると解なしになります。
• よって、　9−k<0　⇒　k>9　と求められます。

このように平方完成は、方程式の解の条件を考える際にも便利なツールです。

▼　３）文章題に挑戦

最後は、文章題での活用です。次のような問題も、平方完成を使えばスムーズに解けます。

• 売上額は「価格 × 個数」なので、
• 売上=x(100−x)=−x²+100x
• 平方完成すると、
• 売上=−(x²−100x)=−(x−50)²+2500
• よって、最大売上は 2500円で、そのときの価格は 50円と分かります。

実戦で使える力を身につけよう

平方完成を味方に

数学の得点力をアップしよう！

二次方程式やグラフの問題で頻出の「平方完成」は、単なる変形技法にとどまらず、数学全体の理解を深める重要なスキルです。このコラムでは、平方完成の基本的な考え方から、定期テストや入試で差がつく応用問題まで、段階を踏んで学んできました。

平方完成をしっかりと自分のものにし、

数学に対する自信と実力を高めていきましょう！

 

---

 

 

お子さまの学習にお悩みの保護者の方へ。

 

 

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。

---

こちら各種SNSでも情報配信中です。参考にしてみてください。

 

 

/

 

この記事は 12人 に閲覧されています。