中学生のための因数分解マスターガイド｜定期テスト・高校受験対策
「因数分解って難しそうで苦手…」
「テストのたびに計算ミスをしてしまう…」
そんな悩みを抱えている中学生は多いはず。でも安心してください。因数分解は“仕組み”を理解して、正しい順番で練習すれば、誰でも得意になれる単元なんです。
このコラム「中学生のための因数分解マスターガイド」では、以下のポイントを中心に、初心者でもわかりやすい形で解説していきます。
-
・共通因数でくくる基本の型をしっかり理解する
-
・公式を覚えて使いこなす練習法
-
・テストや受験に出やすい応用パターンの攻略方法
-
・計画的な勉強法でミスを減らし得点アップを目指す
記事の中では、具体的な例題や図解をたくさん使い、式の変形や考え方をイメージしやすく紹介します。さらに、入試対策として効果的な勉強の進め方や、時間配分のコツも取り上げます。
数学が苦手でも、基礎から少しずつ積み重ねることで、「できた！」という達成感が得られるのが因数分解の魅力です。定期テストや受験勉強の“得点源”にするために、このガイドを一緒に読み進めながら、因数分解の基礎力をしっかり身につけていきましょう。
目次
因数分解って何？【中学数学の基礎】
「因数分解って何？」と聞かれたとき、正しく説明できますか？実は、因数分解は「展開」の逆の計算です。展開で“バラバラにした式”を、もとのかたまりに戻す操作だと思えばイメージしやすくなります。この章では、因数分解の意味や重要性を、例題を交えてわかりやすく解説します。
因数分解の基本の考え方
因数分解とは、「式を“かけ算の形”に直すこと」です。
例えば、
x2+3x
という式を見たとき、両方の項に 「x 」が含まれていることがわかりますよね。そこで「 x 」をくくると、
x(x+3)
と書き換えられます。この「共通している部分を見つけてくくる」動作が、因数分解の最も基本的な考え方です。
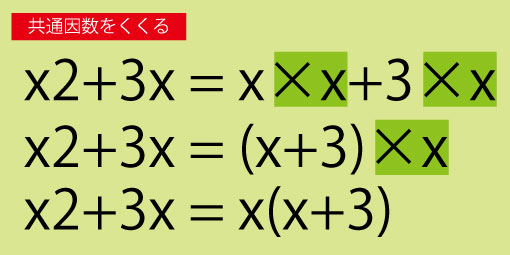
なぜ因数分解が必要なの？
因数分解は、中学数学の基礎から応用まで幅広く使われるスキルです。
-
定期テストでの計算問題はもちろん、
-
高校入試の文章題や関数問題でも必要になることが多い
-
平方根や方程式の学習にも直結する
つまり、因数分解をマスターすれば、数学の幅広い単元をスムーズに解けるようになります。
展開と因数分解はセットで覚えよう
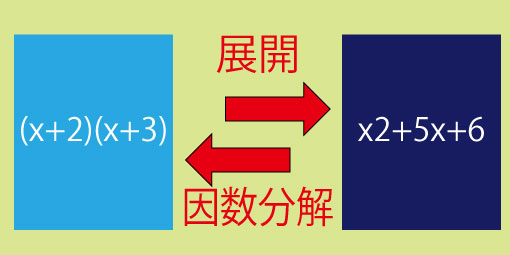
展開と因数分解は表裏一体です。
たとえば、
(x+2)(x+3)=x2+5x+6
という展開を覚えていれば、「 x2+5x+6 」を見たときに、
(x+2)(x+3)
と因数分解できる、というわけです。展開と因数分解を行ったり来たりする練習をすることで、理解がグッと深まります。
よくあるつまずきポイント
因数分解を苦手に感じる原因の多くは、
-
「共通因数を見つけられない」
-
「展開の形を覚えていない」
-
「式を整理する順番がわからない」
の3つです。最初は公式を見ながらでOK。手順を声に出しながら練習すると、自然とスムーズにできるようになります。
次の章では、因数分解のスタートラインである「共通因数でくくる方法」を、具体的な例題を交えて解説していきます。
“共通因数でくくる”をマスターしよう
因数分解のスタートラインは、「共通因数でくくる」ことです。共通因数を見つけられるようになると、式が一気にシンプルになり、解くスピードもアップ！
ここでは、共通因数を見つけるコツと、基本から応用までの練習方法を紹介します。
共通因数って何？
共通因数とは、式の中で共通してかけられている数字や文字のことです。
たとえば、
6x+9
この式は、どちらの項にも「3」が共通して含まれています。だから、「 3 」でくくると
3(2x+3)
となります。「共通しているものを外に出す」という感覚を身につけることが、因数分解の第一歩です。
数字だけじゃない！文字もくくれる
共通因数は数字だけではありません。
たとえば、
x2+3x
この式は、どちらの項にも「 x 」が含まれているので、
x(x+3)
と変形できます。「数字」「文字」「その両方」のどれが共通しているかを探すクセをつけるのがコツです。
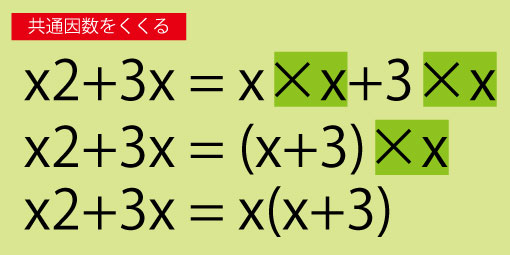
共通因数が2つ以上ある場合
少しレベルアップして、数字と文字の両方をくくる場合を見てみましょう。
4xy+6x
この式は、どちらの項にも「 2x 」が共通しています。だから、
2x(2y+3)
と変形できます。最大公約数を見つけるイメージで考えるとわかりやすいですよ。
応用編 ― “かたまり”をくくる
因数分解に慣れてきたら、“かたまり”をくくる練習もおすすめです。
たとえば、
x(x+2)+3(x+2)
この式は、「 (x+2) 」 という“かたまり”が共通しています。
だから、
(x+2)(x+3)
とくくれます。応用問題や入試問題では、この“かたまり”を見抜けるかどうかが大きなポイントです。
共通因数でくくる練習法
-
色分けを使う：共通因数を赤や青でマークして目立たせる
-
声に出して確認：「共通因数は…3」「外に出す！」と手順を声で確認
-
毎日短時間でも繰り返す：短い式を1日5問だけでも続ける
こうした習慣をつけることで、自然と「くくれる式」が見えるようになってきます。
次の章では、この共通因数のステップを踏まえて、因数分解の公式を使った解法を詳しく解説していきます。
公式で因数分解（基本パターンを覚える）
因数分解のステップアップは、「公式を覚えて使いこなす」ことです。定期テストでも高校受験でも、公式を正確に使えるかどうかが得点のカギを握ります。
ここでは、因数分解の代表的な公式と、その使い方のコツをわかりやすく紹介します。
基本の公式３つを覚えよう
因数分解でまず押さえておきたい公式は、この3つです。
-
共通因数パターン
ax+ay=a(x+y)
-
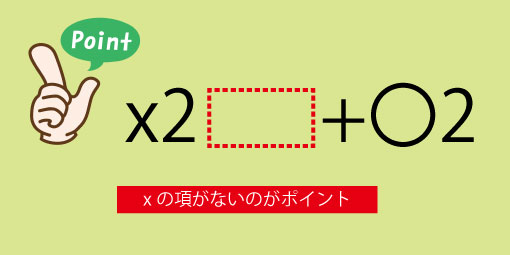
平方差の公式
x2−y2=(x+y)(x−y)
-
展開の逆（たすき型）
x2+(a+b)x+ab=(x+a)(x+b)
この3つをしっかり覚えれば、定期テストの基本問題はほぼ解けるようになります。
足して・かけての見抜き方
公式の中でもよく使うのが、
x2+(a+b)x+ab=(x+a)(x+b)
のパターンです。解くときのコツは、「足して〇〇、かけて〇〇」を見抜くこと。
例えば、
x2+5x+6
の場合、
-
足して5になる数字 → 2と3
-
かけて6になる数字 → 2と3
だから、
(x+2)(x+3)
と因数分解できます。この“足して・かけて”を素早く見抜けるようになると、計算スピードが一気に上がります。
平方差の公式を使いこなす
この平方差の公式も頻出です。
例えば、
x2−9
なら、
x^2−3^2
と考えて、
(x+3)(x−3)
と変形できます。
応用編では、
4x^2 – 25y^2
(2x+5y)(2x−5y)
と変形する問題もよく出題されます。
「2乗の引き算を見たら、この公式！」と条件反射で使えるように練習しておくことが大切です。
公式を覚える練習法
-
声に出して暗唱する：「エックス二乗プラス…」とリズムで覚える
-
例題を繰り返す：短い式で練習して、パターンを体に染み込ませる
-
自分で問題を作る：「x^2+〇x+〇」を自分で設定して因数分解する
ただ暗記するだけでなく、手を動かして使うことで理解が深まります。
次の章では、この公式を使った応用パターンと、テストで差がつく実践テクニックを紹介していきます。
定期テストに出る応用パターンと対策
基本公式が使えるようになったら、次は応用パターンです。定期テストでは、ただ公式を当てはめるだけでは解けない「ひとひねり」した問題が必ず出ます。
ここでは、共通因数をくくる手順から、公式に当てはまらない式へのアプローチ、項の組み合わせ技まで、得点力を一段アップさせるための実践テクニックを解説します。
公式に当てはまらない式へのアプローチ
次に、公式だけでは解けない「ひねった問題」に対応する方法です。コツは、式を変形したり、文字を置き換えたりして“公式が使える形”に近づけることです。
たとえば、
x^4 – 16
このままでは公式に当てはまりませんが、
(x^2)^2 – 4^2
と見れば、平方差の公式「(a^2 – b^2) = (a – b)(a + b)」が使えて、
(x^2 – 4)(x^2 + 4)
と因数分解できます。さらに、x^2 – 4は平方差で、
(x – 2)(x + 2)(x^2 + 4)
と分解可能です。
項の組み合わせ技
A. 2個ずつに分けてグルーピング
4項を2＋2に分け、それぞれで共通因数をくくって“同じかたまり”をつくります。
例１：
2xy+3x+4y+6=(2xy+3x)+(4y+6)=x(2y+3)+2(2y+3)=(2y+3)(x+2)
例２：
ax+ay+bx+by=(ax+ay)+(bx+by)=a(x+y)+b(x+y)=(x+y)(a+b)
ポイント：同じ括弧（例：(2y+3) や (x+y)）を作れる分け方を探すのがコツ。
B. 3＋1に分けて“かたまり”を活かす
3項を先に因数分解→残り1項とまとめて仕上げます。
例１：
x2+5x+6+y(x+2)=(x+2)(x+3)+y(x+2)=(x+2)((x+3)+y)
※ まず 「x^2+5x+6=(x+2)(x+3)」としてから、共通の でまとめます。
例２：（4項化してからグルーピング）
x^2-x-6=x^2+2x-3x-6=(x^2+2x)+(-3x-6)=x(x+2)-3(x+2)=(x+2)(x-3)
※ 係数を分割して4項にし、そこから2＋2グループへ持ち込む手筋です。
C. 対称形を“2＋2”でさばく
例：
x^3+x^2y+xy+y^2=(x^3+x^2y)+(xy+y^2)=x^2(x+y)+y(x+y)=(x+y)(x^2+y)
※ 対称形は「 や「 (x−y) 」といった“よく出るかたまり”を最初に疑うと見つけやすい。
応用パターンの問題は、一見難しそうに見えますが、
-
・共通因数をくくる
-
・公式が使える形に変形する
-
・項を組み合わせてまとめる
この3つの手順でほとんどの問題に対応できます。テスト前には、こうしたパターンを何度も練習し、「見た瞬間に手が動く」状態を目指しましょう。
応用編：置き換え・たすき掛け・高度な整理術
ここまで学んだ基本と応用パターンをマスターしたら、次は応用テクニックです。高校入試レベルや模試でよく出る「ひと工夫が必要な問題」を解くには、置き換え・たすき掛け・高度な整理の3つのスキルがカギになります。
ここでは、それぞれのテクニックと活用法を分かりやすく解説します。
置き換えで式をシンプルにする
複雑な式を見やすくする最強の方法が「置き換え」です。一時的に変数を別の記号で置き換えることで、難しい問題が基本問題に早変わりします。
例：四乗の式
x^4 – 5x^2 + 4
ここで、「 y = x^2 」と置き換えると、
y^2 – 5y + 4
(y−1)(y−4)
→ (x^2 – 1)(x^2 – 4) = (x-1)(x+1)(x-2)(x+2)
とシンプルに分解できます。
ポイント
-
文字の二乗・三乗が混ざる場合は「共通のかたまり」を探す
-
置き換えた後は必ず元の式に戻すのを忘れないこと
たすき掛けで効率的に因数分解
係数が複雑な2次式では、たすき掛けが大活躍します。
例：
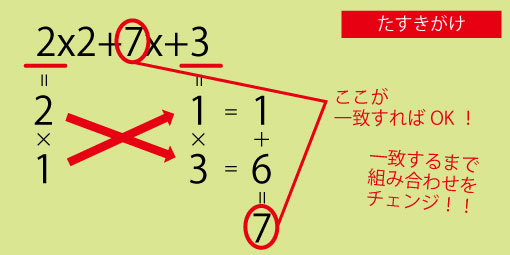
2x^2 + 7x + 3
ステップ１：x^2と定数項の係数になるかけ算の組み合わせを考える
ステップ２：ななめにかけてたす（たすきがけ）
ステップ３：xの項の係数と比較
→数字が合えばOK 合うまで組み合わせをチェンジ！
(2x+1)(x+3)
コツ
-
掛け算の積と真ん中の係数の組み合わせを冷静に探す
-
練習量がカギ！5〜10問連続で解くと一気に感覚が掴めます
高度な整理術で差をつける
定期テストや入試の後半問題では、見た目が複雑でも、式を整理すればシンプルに解ける問題が出ます。
▼共通因数をまとめる
まず全体を見渡して、くくれる文字や数字を最初に抜き出します。
▼項の並び替えで「公式形」に寄せる
x^2 + 6 + 5x
→ x^2 + 5x + 6
と並び替え、
(x+2)(x+3)
に変換する、など。
▼複雑な式を分けて考える
長い式は部分ごとに因数分解→最後にまとめる流れを意識すると、時間短縮にもつながります。
定期テスト＆高校入試への学習計画と勉強法
因数分解をマスターしたら、次は定期テストや高校入試に向けた計画的な学習です。ここまでの基本・応用・応用編テクニックを実際に使いこなすには、日々の学習の積み重ねと効率的な勉強法が重要です。
この章では、学習計画の立て方から、テスト直前の効果的な勉強法までを解説します。
学習計画の立て方
まずは、長期・短期の計画を組み合わせることが大切です。
-
長期計画（1〜2か月）
基礎から応用までの章ごとに分け、1日ごとに練習量を調整します。
例：-
月曜日：共通因数でくくる練習5問
-
火曜日：基本公式の復習と練習
-
水曜日：応用パターン（項の組み合わせ、置き換え）
-
-
短期計画（1週間単位）
テスト範囲や弱点に合わせて集中的に練習。
公式や手順を確認しながら、できない問題を繰り返すのがポイントです。
定期テスト直前の勉強法
テスト前は、短時間で効率的に復習することが重要です。
-
確認ドリルを活用
基本公式・共通因数・応用パターンの確認問題を短時間で解き、理解度をチェック。 -
間違えた問題を重点復習
同じミスを繰り返さないよう、解き直しを必ず行います。 -
時間を測って解く
実際のテストを意識して、制限時間内に解く練習をすると、解答スピードが自然とアップします。
高校入試に向けた学習法
入試では、定期テストよりも複雑な応用問題が出題されます。
対策ポイントは次の通りです。
-
過去問演習
過去問で出題パターンを確認。置き換えやたすき掛けの問題に慣れる。 -
弱点の克服
苦手な公式やパターンをリストアップし、集中して練習。 -
段階的にレベルアップ
基本→応用→応用編テクニックの順に練習。順序を守ることで、焦らず確実に力がつきます。
日々の学習習慣のコツ
-
毎日少しずつ：1日5〜10分でも問題を解く習慣をつける
-
声に出して確認：公式や手順を声に出すと記憶に定着
-
ノート整理：公式・パターン・練習問題を1冊にまとめると復習がラク
小さな積み重ねが、テスト当日の自信につながります。
まとめ
今回のコラムでは、中学生が定期テストや高校入試で得点源にできる因数分解のポイントを、基礎から応用まで丁寧に解説しました。
まずは、共通因数を見つけてくくる基本のステップからスタート。数字だけでなく文字も含めてくくれるようになると、式がスッキリ整理されて解きやすくなります。次に、公式を覚えて使いこなす練習で、平方差や展開公式の逆など、定期テストによく出るパターンをスピーディに解ける力を身につけました。
さらに、応用パターンでは項の組み合わせや置き換え、たすき掛けなどのテクニックを紹介。公式だけでは解けない式でも、ちょっとした工夫で一気に整理できるようになります。文章題や複雑な式への応用も、学んだ手順を順番に踏むことで、難しそうに見える問題も自然と解けるようになります。
そして、定期テストや入試に向けた学習計画では、長期・短期の計画を組み合わせて、日々の練習を積み重ねることの大切さを強調しました。計画的に取り組むことで、自信を持って問題に向かえるようになります。
数学は、少しずつの積み重ねで確実に力がつく科目です。「なんとなく覚える」ではなく、公式やテクニックを理解して手を動かすことが成功のカギ。今日学んだ手順やコツを実際にノートに書いたり、問題を解いたりして、毎日の勉強に取り入れてみてください。最初は時間がかかるかもしれませんが、続けるほどに「解ける！」という手応えが増えていきます。
さあ、因数分解を武器にして、
テストでも入試でも自信をもって挑戦しましょう。
ちょっとしたコツを押さえるだけで、
数学はグッと得意科目に変わります。
今日からの一歩を楽しんで、
着実に力を伸ばしていきましょう！
お子さまの学習にお悩みの保護者の方へ。
当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ！！
こちら各種SNSでも情報配信中です。参考にしてみてください。
/
この記事は 9人 に閲覧されています。
オススメコラム
直前まで手を抜かない！！【1学期期末テスト対策】追い込み集中特訓のご案内
目次1学期期末テスト対策「 追い込み集中特訓 」オススメポイント１）学校ワークなどの提出物にも対応オススメポイント２）長時間学習■ 無料個別相談会・体験受付中 ■ 1学期期末テスト対策 6月に1学期期末テス […]
速さの単位変換を完全攻略！時速・分速・秒速の違いと計算方法を徹底解説
速さの単位変換、なんとなくで解いていませんか？ 「時速、分速、秒速って何が違うの？」「60をかける？割る？どっちだっけ…」そんな風に感じたことはありませんか？速さの単位変換は、小学生から中学生までの算数・数 […]
一次関数「変域」が苦手な中学生へ 定期テスト・高校受験での得点アップにつながるグラフ思考
中学数学の中でも「一次関数の変域」は、多くの中学生がつまずきやすい単元のひとつです。 一次関数そのものは「y＝ax＋b」というシンプルな式ですが、そこに「変域（xやyが取りうる値の範囲）」が加わると、一気に難しく感じてし […]
共通因数＋公式の順で考える
応用問題でも、最初にやることは「共通因数をくくる」ことです。
例えば、
2x^2 + 4x
この式なら、まず共通因数の「 2x 」をくくります。
2x(x + 2)
別の例では、
3x^2y + 6xy^2
この場合も、共通因数の「 3xy 」をくくることで、
3xy(x + 2y)
と整理できます。「共通因数を抜いてから公式を使う」――この手順を徹底することで、計算ミスもぐっと減ります。