高校入試・定期テストで差がつく!二次関数の攻略法とテストでよく出る問題の演習

数学の中でも「関数」は、定期テストや高校入試で必ず出題される、とても重要な単元です。その中でも「二次関数」は、多くの中学生がつまずきやすいポイント。グラフが放物線の形になったり、「最大・最小」を求めたりと、イメージがつかみにくいことが原因です。しかし、実は二次関数は基本をしっかり押さえれば、得点源にできる分野でもあります。
例えば、定期テストでは「グラフの性質」や「変化の割合」などの基礎的な問題が出題されます。ここで確実に点を取れるようにしておけば、安定した得点につながります。
そして高校入試では、「面積」や「最短距離」など、グラフを使った文章題がよく出題されます。一見難しそうに見えますが、出題パターンはある程度決まっています。だからこそ、今のうちに典型問題を練習し、少しずつ応用へとステップアップしていくことが大切なのです。

このコラムでは、二次関数の基本から定期テスト対策、そして高校入試によく出る応用問題までを、ステップごとにわかりやすく解説していきます。
-
第1章では、二次関数の基礎と一次関数との違いを整理し、
-
第2章では、グラフの性質をやさしく解説。
-
第3章では、定期テストの典型問題を確認し、
-
第4章では、高校入試で差がつく応用問題にチャレンジします。
-
さらに第5章では、攻略のコツやケアレスミスを防ぐ方法を紹介し、
-
最後の第6章では、演習を通して実力を定着させます。
さあ、一緒に二次関数を「得点源」に変えていきましょう!
二次関数とは?
基礎からの理解が得点力を高める
二次関数の式に出てくる文字の意味
二次関数の式には「a」「b」「c」という文字が出てきます。これらには大切な役割があります。
-
・a(x²の係数) … グラフの開き方を決めます。aが正なら上に開いたU字型、aが負なら下に開いた∩字型になります。
-
・b(xの係数) … グラフの位置を左右にずらす働きがあります。
-
・c(定数項) … グラフのy切片、つまりy軸との交点を表します。
このように、式の数字の意味を理解することで「グラフの形を頭に描く」ことができるようになります。
一次関数との違いを整理しよう
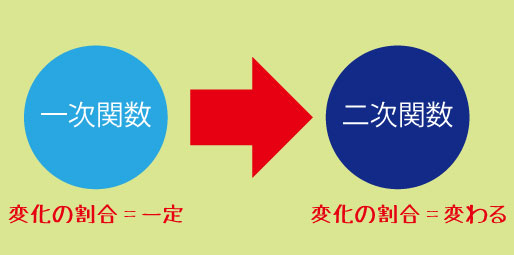
二次関数を学ぶとき、一次関数との違いを整理すると理解がスムーズになります。
-
・一次関数は「変化の割合」が常に一定(傾き)
-
・二次関数は「変化の割合」が場所によって変わる
例えば、一次関数では「右に1動かすと必ずyが2増える」といった関係が成り立ちます。しかし二次関数では、右に1動かすときの増え方がxの値によって違います。ここが「曲線」になる理由です。
二次関数を学ぶと何ができる?
二次関数を学ぶと、グラフを使って「変化」を表現できるようになります。
例えば:
-
・投げ上げたボールの高さと時間の関係(放物線の軌跡)
-
・最大値、最小値を求めることで「効率のよい条件」を見つける
-
・入試問題でよく出る「面積の最大化・最小化」
このように、二次関数は日常生活や実際の現象にも深く関係しており、単なる数字の問題ではないことがわかります。
この章では、二次関数の基礎を整理しました。
-
・二次関数は「x²を含む関数」であり、グラフは放物線の形になる
-
・係数 a、b、c には、それぞれグラフを決める重要な役割がある
-
・一次関数との違いは「変化の割合が一定かどうか」にある
まずはこの基本をしっかり理解しておくことが、定期テストでも高校入試でも得点につながります。次の章では、この二次関数のグラフの性質について、さらに詳しく学んでいきましょう。
グラフの基本性質をマスターする
放物線の形と係数 a の関係
二次関数のグラフは、必ず「放物線」という曲線になります。その形を決めるのが、式の中の a(x²の係数) です。
-
・a > 0(正の数):グラフは上に開いたU字型
-
・a < 0(負の数):グラフは下に開いた∩字型
-
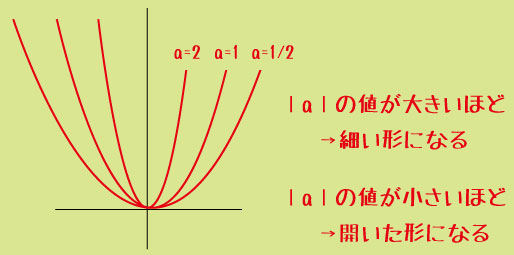
・|a| が大きいほど、グラフは「細く」なり、|a| が小さいほど「ゆるやか」になります
たとえば、y = x² と y = 3x² を比べると、後者の方がグラフが細くなります。この違いをイメージできると、問題の見通しが立てやすくなります。
頂点と軸を押さえよう
放物線には「頂点(グラフの一番高い点 or 一番低い点)」と「軸(グラフの対称の中心となる縦の直線)」があります。
標準形 y = ax² の場合、頂点は (0,0) にあり、軸は x = 0 です。しかし y = ax² + bx + c のように b や c があると、グラフは左右や上下にずれます。
頂点の座標は次の公式で求められます:
x = -b/2a , y = f(-b/2a)
つまり、x座標が -b/2a となる場所に頂点があるのです。この頂点を見つければ、グラフの形をイメージでき、最大値・最小値の問題を解く基礎になります。
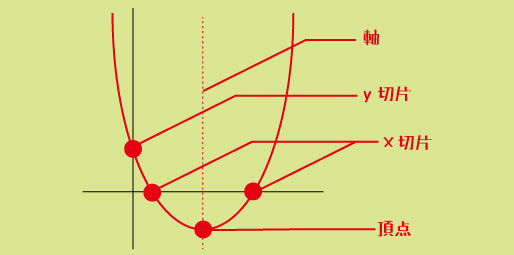
切片・対称性・変域を理解する
グラフを正しく読み取るには、切片や対称性、変域も大切です。
-
・y切片:x=0 のときの値。式の定数 c がそのまま y切片になる。
-
・x切片:y=0 を満たす解。つまり ax²+bx+c=0 の解が x切片の座標になる。
-
・対称性:放物線は必ず軸に対して左右対称になる。これを使うと計算を半分にできることもある。
-
・変域:xの範囲に応じて、yの取りうる値の範囲を決める。特に「最大・最小」を求める問題では欠かせない。
たとえば「xの範囲が0≦x≦5のとき、yの最小値・最大値を求めよ」という問題は、この変域を使う典型問題です。
二次関数のグラフには、必ず押さえるべき性質があります。
-
・aの符号と大きさで放物線の向きや細さが決まる
-
・頂点と軸を求めれば、グラフの中心と形がつかめる
-
・切片、対称性、変域は問題を解く上での基本情報になる
これらを理解すると、ただ式を見て計算するだけでなく「どんな形のグラフになるのか」をイメージできるようになります。次の章では、こうした基本性質をもとに「定期テストで出題される典型問題」を実際に確認していきましょう。
定期テストに出る典型問題パターン
二次関数の学習で「わかる」と「できる」の間には大きな差があります。授業で習ったときは理解できても、いざ定期テストで問題を解こうとすると「どの公式を使うのか?」「どこから手をつければいいのか?」と迷ってしまうことが多いのです。
実際、定期テストや高校入試では「パターン化された典型問題」が繰り返し出題されます。つまり、そのパターンをしっかり押さえておけば得点が安定し、応用問題にも強くなります。
この章では、テストに必ず出る典型問題を整理し、攻略のポイントを解説していきます。
グラフの読み取り問題
二次関数の最も基本的な問題は「グラフを見て情報を読み取る」ものです。
例えば、
-
・頂点の座標を求める
-
・軸の式を答える
-
・グラフが通る点の座標を利用する
といった問題がよく出ます。
ここでは、式を覚えるよりも「グラフの形をイメージできるか」がカギです。特に、放物線が「上に開く」か「下に開く」か、頂点がどの位置にあるかを瞬時に判断できるようにしましょう。
解の個数・範囲を問う問題こにタイトル
定期テストで必ず出るのが「二次方程式との関係」です。
例えば、
-
・ax^2+bx+c=0 の解の個数を判定する
-
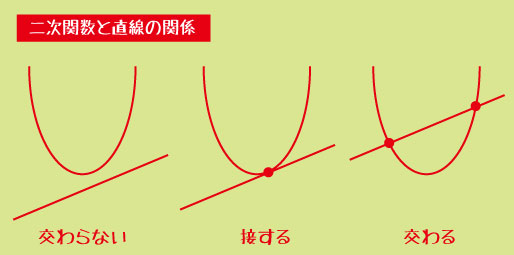
・y=ax^2+bx+c と直線の交点の個数を求める
-
・関数が取りうる値の範囲を答える
といった出題です。
このとき重要なのが「判別式(D)」や「最大・最小の考え方」です。
判別式 D=b^2-4ac を使えば、グラフがx軸と何回交わるかを一発で判断できます。また、値の範囲は「頂点のy座標」と「グラフの開き方」で決まります。
ここを理解すると、文章題や応用問題にもつながります。
文章題(応用パターン)
テストで点差がつくのは「文章題」です。
代表的なのは、
-
・二次関数を使った図形の面積問題
-
・投射運動や水の量の変化をモデル化する問題
-
・最大値、最小値を利用する最適化問題
などです。
例えば「あるボールを投げ上げたときの高さを二次関数で表す」といった問題では、時間をx、高さをyとした関数を作り、最大値を使って「一番高い高さ」を求めます。こうした問題は、ただ公式を覚えているだけでは解けません。「状況をグラフに置き換える」練習が大切です。
定期テストでは、
-
1)グラフの読み取り
-
2)解の個数や範囲
-
3)文章題(応用パターン)
の3本柱で問題が構成されています。これらは高校入試でもそのまま出題されるため、早いうちからパターンを身につけておくことが得点アップの近道です。
特に文章題は、生徒が苦手意識を持ちやすい部分です。塾で丁寧に「図にして考える方法」を身につければ、苦手を得意に変えることができます。
高校入試でよく出る応用問題を攻略する
高校入試で差がつくのは、実は「難しい計算問題」よりも「応用問題」です。基礎的な計算はどの受験生もある程度できるため、得点差は文章題や図形を絡めた二次関数の応用問題で大きく開きます。
しかし、多くの生徒は「問題文をどう式に変換すればいいのか分からない」とつまずいてしまいます。
そこで重要なのが「パターンを整理しておくこと」です。塾では一つひとつのパターンを丁寧に解説し、図に描きながら理解を促すことで、初見の問題でも対応できる力を育てていきます。
図形との融合問題
二次関数と図形の組み合わせは入試の定番です。
例えば、
-
・放物線と直線で囲まれた部分の面積を求める
-
・二次関数のグラフとx軸で囲まれる面積を求める
といった出題です。これらの問題では「どこを面積として計算するのか」をイメージできるかどうかがカギとなります。単純な計算力だけでなく、図形的なセンスも必要とされるため、独学では苦手意識が強くなりやすい分野です。

最大値・最小値を使う最適化問題
入試で必ずといっていいほど出るのが「最大値・最小値を利用する問題」です。
代表的なのは、
-
・投げ上げたボールの高さを求める問題
-
・ある条件のもとで一番大きな面積、体積を求める問題
-
・コストや距離などを最小にする問題
です。例えば「ある長方形の面積を最大にするときの辺の長さを求めよ」という問題では、長方形の辺を文字で表し、二次関数の形に変換して最大値を求めます。こうした問題は「文章を式に直す力」と「グラフの意味を理解する力」が同時に求められます。
文章題に強くなるための練習法
応用問題を攻略するには、やみくもに問題集を解くだけでは不十分です。特に中学生は「なぜこの式になるのか」を理解しないまま解き方だけを暗記しがちです。その結果、少し形が変わった問題に出会うと手が止まってしまいます。
塾での指導では、
-
1)問題文を読んだら「まず図にする」
-
2)その図を見ながら「条件を式に直す」
-
3)最後に「グラフの性質を使って答えを導く」
というステップを繰り返し練習させます。特に「自分で図を描く力」がつくと、応用問題に対する抵抗感が一気になくなります。
高校入試で差をつけるのは、基礎ではなく応用問題です。
-
・図形との融合
-
・最大値、最小値の最適化
-
・文章題の処理能力
といったテーマを克服することで、合否に直結する得点を安定して獲得できます。
保護者の方にとって心配なのは「うちの子は応用問題になると手が止まってしまう」という点かもしれません。しかし、それは決して才能やセンスの問題ではなく、「問題を図にし、整理する練習の有無」によって大きく変わります。塾で体系的に指導することで、初めて見る問題でも落ち着いて解ける力を養うことができます。
解き方のコツとケアレスミス防止法
二次関数の問題は「解き方を知っているかどうか」だけでなく、「どのように取り組むか」で得点が大きく変わります。
実は入試や定期テストで失点してしまう多くの原因は、難しい問題ではなく「ケアレスミス」です。符号を間違えたり、計算過程を飛ばして書いて見落としたり…。これらは、ほんの数点に見えても合否や順位を分ける大きな差になります。
そのため大切なのは、日ごろから「正しい解き方の習慣」を身につけることです。塾での個別指導だけでなく、家庭学習での小さな工夫がケアレスミスを防ぎ、確実な得点力へとつながります。
問題を分解して解く習慣
二次関数の問題は、一気に答えを出そうとすると間違いが増えます。そこで効果的なのが「問題を小さなステップに分解する習慣」です。
例えば、グラフと直線の交点を求める問題なら、
-
1)二次関数の式を確認する
-
2)直線の式を整理する
-
3)連立方程式にして二次方程式を作る
-
4)解の公式や因数分解で解を出す
という流れを確認しながら一つずつ進めます。
こうした手順を習慣化することで、どんな問題でも「迷わず、同じ道筋」で解けるようになります。これは家庭学習でも練習できるポイントです。
ノートの使い方で差がつく
ケアレスミスの多くは「途中式を書かないこと」が原因です。頭の中で計算を省略してしまうと、符号や数字の取り違えが起こりやすくなります。
そこで塾では「途中式を必ず書く」ことを徹底させています。特に二次関数では、式変形や平方完成、因数分解などのステップが多く、飛ばすと確実にミスにつながります。
家庭学習でも、
-
・1行ずつ丁寧に式を書く
-
・計算の区切りごとに確認する
-
・答えだけでなく、考え方をノートに残す
といった習慣を身につければ、テスト本番でも安心です。
ケアレスミスを防ぐチェックリスト
家庭学習での“習慣づけ”をさらに強化するために、「ケアレスミスチェックリスト」を作るのも効果的です。
例えば、
-
・符号の確認(+と-を逆にしていないか?)
-
・因数分解の展開ミスはないか?
-
・頂点や軸の計算で割り算を間違えていないか?
-
・最後に単位や答えの形式を確認したか?
こうした項目を1問ごとに確認することで、自然と注意力が高まります。塾では個別に「その子がしやすいミス」を洗い出して指導できるため、保護者の方からも「家庭学習の質が変わった」と喜ばれることが多いのです。

二次関数の攻略において重要なのは、難しい公式を覚えることよりも「日ごろの解き方の習慣」を整えることです。
-
・問題を分解して解く流れを守る
-
・ノートに途中式を必ず残す
-
・チェックリストでミスを防ぐ
これらを徹底することで、着実に得点力が積み上がります。
イマナビでも、授業中の個別指導で「正しい解き方の型」を身につけさせ、家庭学習でも同じ習慣を繰り返すように指導しています。ただの暗記や付け焼き刃ではなく、「本番で確実に点を取る力」へと結びつけることが大事です。
得点アップのステップ
ここまで二次関数の基礎から応用までを整理してきました。理解を深めることはもちろん大切ですが、「テストで点数を取る」ために欠かせないのは、実際に演習を重ねることです。
スポーツと同じで、理論を知っているだけでは試合に勝てません。基礎を理解した上で、実戦形式の練習を繰り返すことで初めて「使える力」に変わります。二次関数も同じで、授業で習った内容を演習で反復し、テスト本番で落ち着いて解ける状態にしておくことが得点アップの近道です。
基礎問題の反復で「土台」を固める
演習を始めるときに大切なのは、まず「基礎問題の徹底反復」です。
例えば、
-
・頂点、軸の求め方
-
・放物線の開き方とグラフの形
-
・判別式を使った解の個数の確認
といった内容です。これらは入試の応用問題を解くための“土台”であり、ここが曖昧だと少し複雑な問題に出会ったときに立ち止まってしまいます。
基礎問題を繰り返し解くことで、「これはこうすればいい」と自動的に手が動く状態を作りましょう。

標準問題でパターンを整理する
次のステップは「標準問題」でよく出るパターンを整理することです。
例えば、
-
・グラフと直線の交点を求める問題
-
・値の範囲を答える問題
-
・二次関数を文章に置き換えた問題
といった出題です。これらは定期テストや入試で必ず出る「典型問題」であり、得点源となる部分です。
ここで重要なのは、「ただ答えを出す」ことではなく、「どういう考え方をしたか」を振り返ることです。解き方をノートに残しておけば、後で見直したときに「このパターンはこの手順で解く」と整理でき、次の演習に生きてきます。
応用問題で本番力を養う
基礎・標準が固まったら、最後に「応用問題」で実戦力を養います。
応用問題では文章題や図形との組み合わせなど、複数の知識をつなげる力が求められます。最初は難しく感じますが、基礎と標準の力があれば必ず取り組めるようになります。
ここで効果的なのは「解き直しの習慣」です。間違えた問題を解き直すことで、弱点が浮き彫りになり、それを次につなげることができます。
演習の質は「間違えをどう活かすか」で決まります。塾では、間違えた原因を一緒に分析し、家庭学習でも同じステップで復習できるようにサポートしています。

二次関数で得点力をつけるためには、
-
1)基礎問題で土台を固める
-
2)標準問題でパターンを整理する
-
3)応用問題で実戦力を養い、解き直しで弱点を克服する
というステップが必要です。
この流れを日ごろの学習に組み込むことで、定期テストだけでなく高校入試でも安定した得点を取れるようになります。
そして何より大切なのは、このサイクルを「継続すること」です。一度で身につくものではなく、習慣として取り組むことで確実に成果が表れます。
イマナビでも、この演習サイクルを授業と家庭学習の両方で徹底できるようサポートしています。だからこそ、生徒が「やり方は分かるけど続かない」という壁を乗り越え、日ごろの学習習慣を通じて本番で結果を出せるようになるのです。
今回のコラムでは、中学生が二次関数で定期テストや高校入試の得点力を伸ばすためのステップを、基礎理解から応用演習まで順を追って解説しました。
二次関数は、公式や計算方法を覚えるだけでは得点に直結せず、グラフの性質や問題の構造を理解し、日々の学習習慣として反復することが非常に重要です。学んだ内容を「日ごろの学習の中でどのように整理し、実践するか」が、安定した得点を生むカギとなります。
二次関数の基礎理解とグラフの基本性質を確認しました。ここでの学習は単なる知識の確認にとどまらず、問題を見たときに頭の中で放物線の形や頂点、軸、切片をイメージできるようになるための準備です。家庭学習では、このイメージ化の練習を日ごろから繰り返すことが重要です。
定期テストや高校入試で頻出の典型問題や応用問題を取り上げました。特に文章題や図形との組み合わせ問題は、「問題文をどう式に変換するか」を日ごろから意識して練習しておくことが必要です。家庭学習で毎回少しずつ演習し、間違えた部分をノートに整理する習慣をつけることで、応用問題でも迷わず解答できる力が育ちます。
解き方やケアレスミス防止のポイントを紹介しました。解法のステップを分解して問題に取り組むこと、途中式を必ず書くこと、チェックリストを使ってミスを確認することなど、日常的に取り組める小さな習慣が得点力を確実に伸ばします。
基礎→標準→応用の演習サイクルを確認しました。日ごろの学習をこの順で積み重ねることで、理解を確実に定着させ、テスト本番での得点力につなげることができます。ここでも重要なのは、「毎日の学習を習慣化すること」です。
イマナビでは、授業で理解した内容を家庭学習で定着させるサポートを徹底しています。徹底個別の指導により、一人ひとりの弱点や課題に合わせた演習を組み、家庭学習指導で日ごろの学習習慣を強化することで、「わかる」から「できる」に変える学習環境を提供しています。この仕組みを通じて、生徒は定期テストでも入試でも安定して得点を伸ばせる力を身につけることができます。
イマナビでは、その習慣づけを一人ひとりに合わせて支えることで、確実に得点力を伸ばすお手伝いをしています。
お子さまの学習にお悩みの保護者の方へ。

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ!!
こちら各種SNSでも情報配信中です。参考にしてみてください。
/
この記事は 2,201人 に閲覧されています。
.jpg)




二次関数とは何か?
二次関数とは「変数 x の2乗を含む関数」のことを指します。一般的には、
y = ax^2 + bx + c (a ≠ 0)
という形で表されます。この「2乗(x²)」があることで、グラフが直線ではなく「放物線」という曲線になります。
例えば、一次関数 y = 2x + 3 のグラフはまっすぐな直線ですが、二次関数 y = x^2 のグラフは「U字型の曲線」となります。この違いをイメージできることが、学習の第一歩です。