中学数学の公式を完全網羅!定期テストで点が取れる最強まとめ【図形・方程式・関数】

中学数学の定期テストでは、多くの生徒が
「公式を覚えているつもりなのに、点数が伸びない」
という悩みを抱えています。実はこの原因、「公式を暗記しているだけ」になってしまっていることが大きいのです。
公式は覚えるだけでは得点につながりません。
“どの場面で使うのか”“どう組み合わせるのか”まで理解してはじめて、確実に点が取れるようになります。

そこで本コラムでは、「中学数学の公式を完全網羅!定期テストで点が取れる最強まとめ【図形・方程式・関数】」というテーマで、中1〜中3までの全公式を分野別にわかりやすく整理しました。
さらに、テストに直結する「使い方」や「ミスしやすいポイント」まで丁寧に解説します。
中学生はもちろん、保護者の方や指導する先生にも役立つ、“一生使える公式のまとめ”を目指した内容です。
例えば、三角形の面積公式「1/2 × 底辺 × 高さ」を覚えていても、どれが高さなのか判断できなければ問題は解けません。
一次関数でも、「y=ax+b」を知っていても、「a が何を表すのか」「b はどんな意味なのか」が曖昧なままでは文章題に太刀打ちできません。
つまり、
公式=覚えるものではなく、使いこなすもの
という視点が重要なのです。
このコラムの特徴
- 1)分野別に必要な公式をすべて整理(計算・関数・図形)
- 2)定期テストの頻出パターンを徹底分析
- 3)使い方のポイントやミス例を具体的に紹介
- 4)図解でイメージしやすく、丸暗記に頼らない理解をサポート
本記事では、単に公式を並べるだけではなく、「なぜその公式が必要なのか」「どんな場面で使うのか」まで丁寧に掘り下げていきます。
最後の第6章では、実際の定期テストを想定した「使い方の攻略法」まで解説するため、読み終わったころには、“公式を覚える” → “使える”にレベルアップできる内容になっています。
数学が苦手な生徒でも、公式の意味がわかると、一気に得点源に変わっていきます。
ぜひ、このコラムを活用して、次の定期テストで高得点をめざしましょう。
目次
第1章|中学数学の公式を攻略する前に
覚え方・使い方のコツ
中学数学の定期テストでは、公式を「知っている」だけでは十分ではありません。「どの場面で使えばいいのか」「どうやって問題文から読み取るのか」という“使いこなす力”がなければ、点数につながらないからです。
まずは、公式学習のつまずきを防ぎ、これからの学習をスムーズにするための“基本姿勢”をまとめていきます。
公式を覚えやすくする3つのコツ
① 意味をセットで覚える
公式は「なぜそうなるのか」を理解して覚えると、忘れにくくなります。例えば台形の面積公式も、“平行四辺形を半分にした”というイメージがあれば、式を忘れても導き出せます。
② 類題を続けて解く
同じタイプの問題を連続で解くことで、「あ、このパターンはこの公式を使うんだ」と判断力が身につきます。定期テストでも、公式の“適用パターン”を把握しているかが得点の差になります。
③ 図に直す
関数や図形は、頭の中だけで考えると混乱します。問題文を読んだらまず、式や状況を“図”に表す習慣をつけてください。特に図形問題では、図を書くだけで正答率が大きく上がります。
定期テストでよくある失点パターン
定期テストでは以下のようなミスが頻発します。
-
公式を思い出せない
-
どの公式を使うか判断できない
-
途中式で計算を間違える
-
図を書かないために条件を見落とす
-
公式の“高さ”や“角度”などの意味を勘違いする
これらの失点は、すべて 「理解不足」と「整理不足」 によって起こります。つまり、正しい学び方さえ身につければ、防ぐことができるのです。
「どの公式を使うか」判断する練習が成績を伸ばす
数学が苦手な生徒の多くは、公式自体は覚えていても、選び方でミスします。
- 「これは一次関数の問題? それとも比例?」
- 「どの長さが高さとして使える?」
こうした判断力は、問題を解く中で少しずつ身につきます。
特におすすめなのは、
- ・例題を1問解く
- ・解説を読み、なぜその公式を選んだか確認する
というサイクルです。これを繰り返すだけで、正しい場面判断ができるようになります。
このコラムの活用方法
本コラムは、次の流れで学びやすい構成になっています。
-
1)分野別に公式を完全整理(計算・関数・図形)
-
2)重要度つきで、覚える優先順位が明確
-
3)定期テストでよく出る 頻出パターン を紹介
-
4)図解で視覚的に理解しやすい
-
5)最終章で “公式を使う力” を鍛える実戦演習つき
この順で読み進めれば、「覚える → 理解する → 使える」という、数学で最も重要な学習プロセスを自然と身につけられます。
次章からは、計算・関数・図形の公式を体系的に整理しながら、定期テストで点が取れる力を一緒に身につけていきましょう。
第2章|計算(数と式)の重要公式まとめ
文字式・因数分解・平方根
計算分野は、中学数学の中でも特に“定期テストの得点を大きく左右する”分野です。文字式・方程式・因数分解・平方根──どれも一見バラバラの内容に見えますが、「式を整理する」「意味を読み取る」という共通の力が必要になります。
この章では、各分野の公式と基本の考え方、そして失点しやすいポイントまでまとめていきます。
文字式の基本:同類項・分配法則・式の値
▼同類項の計算
文字式では、文字が同じ項同士をまとめます。たとえば、
3a + 5a = 8a
2x² – x² = x²
というように、文字や次数が一致しているものだけを足し引きできます。
■ よくあるミス ■
- ・x と x² をまとめてしまう
- ・マイナスの符号を見落とす
▼分配法則(展開)
計算の最も基本となる法則です。
a(b+c)=ab+ac
を軸に、次のような形も同じ考え方で広がります。
〈例〉
(x+3)(x+2)=x2+5x+6
展開公式を覚える前に、「1つずつかける」イメージを持つことが大切です。

▼式の値の求め方
与えられた文字に数字を代入し、丁寧に計算していきます。カッコをつけずに代入すると符号ミスが起こりやすいので、( )に入れて代入する癖が得点アップのポイントです。
方程式の解き方:移項・比例式の変形
▼一次方程式の基本
ポイントは以下の3つ:
- 1)x のついた項を左へ、数字を右へそろえる
- 2)移項は「符号が変わる」ことに注意
- 3)最後に x の係数で割る
〈例〉
3x–5 = 10→ 3x = 10+5 ※移項で符号が変わる!
→ 3x=15
→ x = 5
▼比例式の変形(内項の積=外項の積)
比例式 a/b=c/d は、
ad = bc
として変形できます。
これはテストに非常によく出ますが、両辺に「b と d をかけた」結果であることを理解しておくと忘れません。
因数分解:基本の公式とポイント
因数分解は展開の逆の操作と考えると理解しやすくなります。
▼共通因数でくくる
最初に「全ての項に共通する数や文字がないか」を確認しましょう。
〈例〉
3×2+6x=3x(x+2) ※各項に「3」と「x」が共通している!
▼因数分解 基本の3公式
- 平方差
a2–b2=(a+b)(a–b) - 完全平方(+)
a2+2ab+b2=(a+b)2 - 完全平方(−)
a2–2ab+b2=(a–b)2

これらを見分けるコツは、
- 「最初と最後がどちらも2乗の形か?」
- 「真ん中の項が2abの形になっているか?」
をチェックすることです。
平方根:√の性質と有理化
▼√の基本性質
-
・√a × √b = √(ab)
-
・√a ÷ √b = √(a/b)
-
・√(a²) = a(a が正の数のとき)
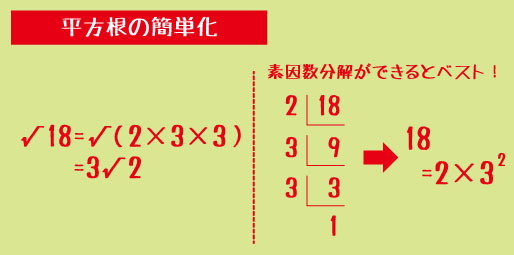
また、
√18 = √(9×2) = 3√2
という形に直すことが定期テストでは必須です。
▼有理化の公式
分母に√が残っているときは「分母の√を消す」操作を行います。これを有理化といいます。
〈例〉
ここでもカッコを忘れるとミスになるので要注意です。
テストで頻出のミスと防ぎ方
-
符号の見落とし:特に「−」が絡むとミスしやすい
-
カッコをつけずに代入する
-
式変形の順序を間違える
-
因数分解で公式の見分けができない
-
平方根の簡単化を忘れる
これらは、いずれも「丁寧に書く」ことで8割防げます。
特に、中学生が最も多く落とすのが「符号ミス」。途中式を必ず書き、「−(マイナス)」の扱いに注意しましょう。
計算分野は、数学の土台になる力です。文字式・方程式・因数分解・平方根は、一見別の分野のようでいて、どれも「式を読み取って整える」力で共通しています。
この章の公式とポイントを押さえておけば、定期テストでの計算パートは確実に得点源になります。
次の章では、グラフで差がつきやすい“比例・反比例・一次関数”の公式を整理していきます。
第3章|比例・反比例と一次関数の公式
グラフの読み方・式の作り方
比例・反比例、そして一次関数は、中学数学の中でも「グラフ」と「式づくり」がセットで問われる単元です。公式自体はシンプルですが、「どの公式を使う?」「何を求めればいい?」という判断力が点数差につながります。
また、比例と一次関数の区別が曖昧なまま問題を解いていると、式の作り方や読み取りでミスが増えてしまいます。
この章では、グラフの意味→式のつくり方→文章題への応用という流れで、テストで点が取りやすい理解方法を整理します。
比例と反比例の基本:式・定数の求め方を理解する
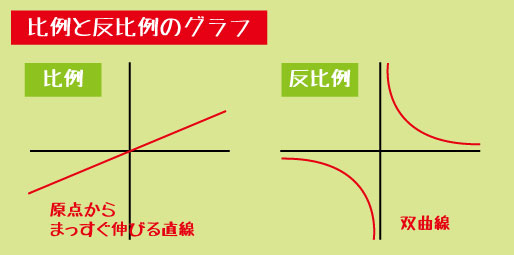
▼比例
y=ax
“出発点は必ず 0” という特徴があります。比例定数 a は、
a=y/x
で求められ、グラフは原点からまっすぐ伸びる直線です。
▼反比例
y=a/x
反比例定数 a は、
a=x×
で求められます。グラフは双曲線で、原点は通りません。
一次関数の公式:切片と傾きの意味から理解する
▼一次関数の基本式
y=ax+b
の形で、比例を発展させたものです。
●傾き(a)の意味
x が1 増えたとき、y がどれだけ増減するかを表す値。
→「変化の割合」とも言われます。
●切片(b)の意味
x=0 のときの y の値。
→ グラフが y 軸と交わる位置。
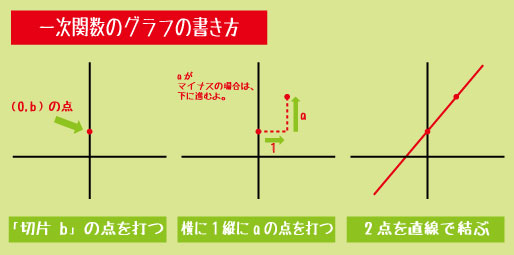
●一次関数グラフの書き方
-
1)まず「切片 b」の点を打つ
-
2)傾き a を使って、x方向に1進んで、上(または下)に a進んだ点を取る
-
3)2点を直線で結ぶ
中学生がよく陥るミスは、先に「適当に」点を取ろうとすること。一次関数は 「切片 → 傾き」 の順に書けば、必ず正しく描けます。
▼2点から一次関数の式を作る公式
2点 (x1,y1),(x2,y2)からは、
a=(y2−y2)/(x2−x1)
という流れで式が作れます。
文章題に強くなる“増加量”と“変化の割合”の公式的アプローチ
一次関数の文章題のほとんどは、
「どれだけ増えた? → 割合は?」
の見方ができると簡単になります。
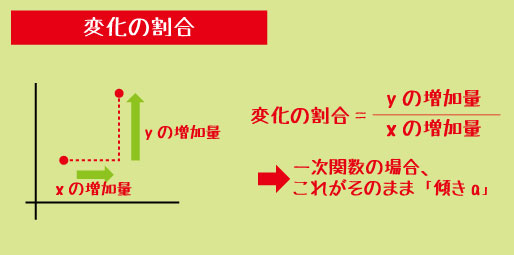
▼増加量
増加量=後の値−前の値
▼変化の割合
変化の割合=(yの増加量)/(xの増加量)
これはそのまま「傾き a」につながります。
- ・距離と時間のグラフ
- ・代金と個数の関係
- ・水位の増減
など、実生活系の文章題のほぼすべてで使える視点です。
テストで差がつく問題と失点パターン
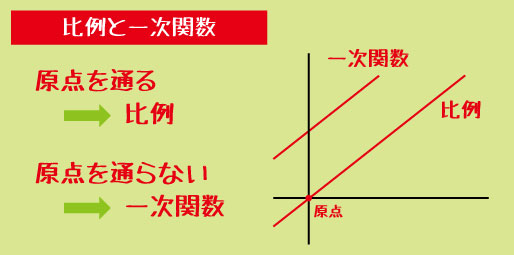
▼「比例なのか一次関数なのか」を間違える
- ・原点を通る → 比例
- ・原点を通らない直線 → 一次関数
グラフ問題でも文章題でも、ここを見分けるだけでミスは激減します。
▼「x の値を読み間違える」
グラフ読み取りで多発。
- ・目盛りが1でない
- ・小数や分数表記
といった設定に惑わされないよう、まず目盛りチェックが必須です。
比例・反比例・一次関数は、「グラフ」「式」「文章題」の3つがひとつにつながった単元です。大切なのは、公式を丸暗記するのではなく、定数 a の意味・傾き b の役割・グラフの形をセットで理解すること。
この章のポイントが身につくと、計算だけでなく文章題の正答率が一気に上がります。
次の章では、図形分野の「読めばそのまま使える公式」を整理し、得点源にしていきましょう。
第4章|図形の基本公式まとめ
角度・合同・相似・作図のポイント
図形分野は
- 「覚える公式が多い」
- 「どこで使うのかわからない」
と感じやすい単元です。しかし実は、角度、合同、相似、作図はすべて“考え方の土台”が共通しており、ポイントを押さえると定期テストで大きな得点源になります。
特に、角度の基本(同位角・錯角)、三角形や多角形の内角・外角の性質、合同や相似の条件、作図の基本操作は、すべて問題の“スタート地点”になる重要知識です。
この章では、公式をただ並べるのではなく、
- 「どんな場面で使うのか」
- 「どう判断するのか」
という視点で整理し、実戦で迷わない力を身につけていきます。
こ度の基本公式:平行線・三角形・多角形を一気に整理
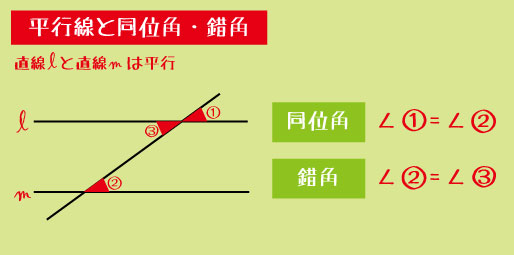
▼同位角・錯角
平行線があるとき、同位角・錯角は必ず等しくなる。
→ 角度問題の“最初の突破口”。
▼三角形の内角和
180°
どんな三角形でも、3つの角の和は180°。
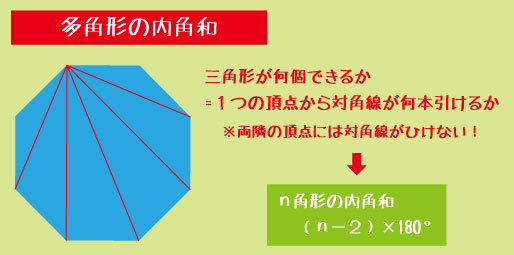
▼多角形の内角和
n角形の内角和
(n−2)×180°
四角形なら 2×180°、五角形なら 3×180°。
▼外角の性質
多角形の外角の和は360°(どんな形でも一定)
→ 正多角形の「1つの外角=360°÷辺の数」にそのまま使える。
合同の条件:形と大きさが全く同じになる理由を理解する
合同とは「形も大きさも全く同じ」。
証明問題の基礎でもあり、条件を暗記するだけでも点数が安定します。
▼合同条件(3つ)
- ① 3辺がすべて等しい
- ② 2辺とその間の角が等しい
- ③ 1辺とその両端の角が等しい
これらに当てはまれば、図形は完全に一致します。
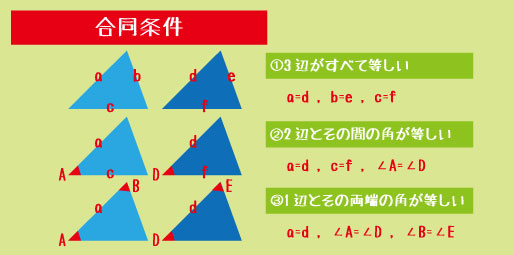
「間の角かどうか」が判断ミスのポイント。
例:SASで必要なのは“間に挟まれた角”で、外側の角ではない。
相似の条件:形が同じで拡大縮小した関係をつかむ
相似とは「形は同じ・大きさは違う」。
見た目だけで判断しようとすると失敗するため、条件を公式として理解することが重要です。
▼相似の条件
- ① 対応する辺の比がすべて同じ
- ② 1つの角とその両側の辺の比が同じ
- ③ 2つの角が等しい
▼相似比・面積比・体積比
相似な図形では以下が必ず成り立つ。
相似比:k
面積比:k
体積比:k3 (立体では)
面積比でミスをする原因は、「k の二乗」を忘れてしまうこと。
→ “長さ→2乗で面積→3乗で体積” をセットで覚える。
作図の3大パターン:「垂直」「角度」「距離」の基本をおさえる
作図は“操作”自体は難しくなく、ポイントを知っていれば高得点がねらえます。
▼① 垂直二等分線
・2点を結ぶ線分の垂直方向で、2点からの距離が等しい点の集まり。
→ コンパスで「同じ半径の円弧」を描くのが基本。
▼② 角の二等分線
・角の2辺からの距離が等しい点の集まり。
→ コンパスを使って2つの“交点”を作るのがポイント。
▼③ 距離一定の点(円の作図)
・点Aからの距離が一定の点は、中心A・半径r の円周になる。
→ 円の性質をそのまま使う単純パターン。
作図でよくあるミスは、「どこが中心で、どこが半径なのかを勘違いすること」。
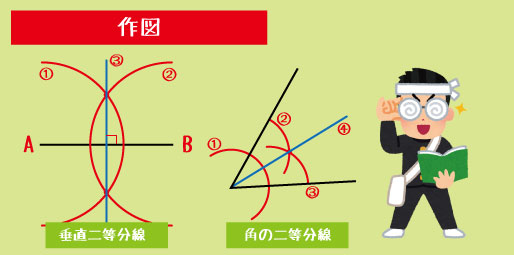
間違えやすいポイントと混同しがちな概念を整理
▼相似比と面積比、合同と相似の取り違え
-
「相似比=面積比」と思ってしまう
→ 面積は 2乗! -
合同は「形も大きさも同じ」
-
相似は「形は同じ・大きさは違う」
テストでは、この区別を問う問題が非常に多いです。
混乱したら、必ず
- 「大きさまで同じ? → 合同」
- 「形だけ? → 相似」
と考えるクセをつけましょう。
角度・合同・相似・作図は、中学図形の“基本4分野”。どれもテストで必ず出てきますが、見るべきポイントは決して多くありません。
大切なのは、公式の丸暗記ではなく、どの場面でどの性質が使えるのかを判断すること。特に、平行線の角度・合同条件・相似比の扱い・3つの作図は、「わかっているつもりで落とす」典型分野です。
この章の内容を中核に、次章ではさらに応用度の高い“立体図形と体積・表面積の公式”をまとめていきます。
第5章|平面図形・空間図形の公式
面積・体積・表面積を完全攻略
面積・体積・表面積の公式は、一見すると「たくさんあって覚えるのが大変」と感じる分野です。しかし、実はすべての公式が“基本の考え方”からつながっているため、意味を理解すれば暗記に頼らず確実に使いこなすことができます。
例えば、三角形の面積の
1/2×底辺×高さ
は、平行四辺形の半分になることから導かれますし、円柱の体積
πr2h
は、「底面の円の面積 × 高さ」というシンプルな発想です。
この章では、平面図形と空間図形をまとめて整理し、公式を「覚える」から「使える」へと変えるポイントを解説していきます。
平面図形の面積公式:基本形を意味から理解する
▼三角形の面積
1/2×底辺×高さ
理由:平行四辺形にするとちょうど半分。
▼平行四辺形の面積
底辺×高さ
高さは“底辺に垂直な長さ”である点に注意。
▼台形の面積
(上底+下底)/2×高さ
平均の長さ×高さのイメージ。図にするとすぐ理解できる。
▼円
面積:πr2 / 半径×半径×円周率
円周:2πr / 直径×円周率
→ 面積と円周は「r(半径) を使う」という点でセット。
空間図形の体積:底面積×高さに統一して理解
空間図形の体積は、実はほとんどすべて
底面積×高さ
で統一できます。(円錐だけ “1/3” が付く)
▼直方体
縦×横×高さ
= 底面積(長方形)×高さ
▼三角柱
底面積(△)×高さ
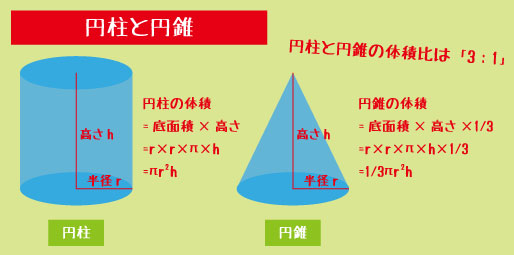
▼円柱
πr2h / 円の面積 × 高さ
▼円錐
1/3×底面積×高さ
→ 円柱の体積の “1/3” になる理由が分かると忘れない。
▼球
4/3πr3 / 半径×半径×半径×円周率×4/3
球の公式は丸暗記になりがちだが、“円が回転してできる立体”の延長として捉えると理解しやすい。
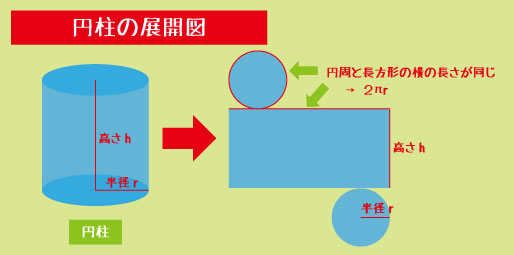
表面積の攻略:立体を展開図で捉えると失敗しない
表面積は“展開する”イメージを持つと理解が早い。
▼円柱の表面積
・上下の円:2 × πr²
・側面:円周 2πr × 高さ h(=長方形)
→ 2πr2+2πrh
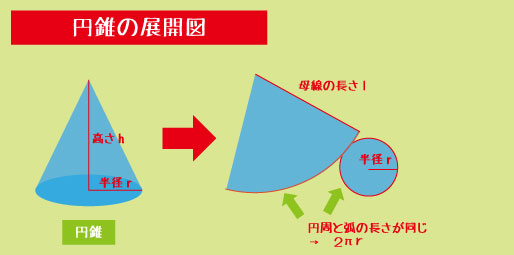
▼円錐の表面積
・底面:πr²
・側面:円弧の面積(=扇形)
→ πr2+πrl (※ l=母線の長さ)
▼球の表面積
4πr2 / 4×円周率×半径×半径
表面積では
- 「どこまで展開するのか」
- 「半径?母線?高さ?」
の混同が非常に多い点に注意。
よくあるミスと補助線の入れ方のコツ
■ミス例
- ・三角形の高さの位置を間違える
- ・円の半径と直径を混同
- ・円錐の “l(母線)” を h(高さ)と勘違い
- ・体積か表面積かを読み違える
- ・単位(㎝²、㎝³)をつけ忘れる
■補助線のコツ
- ・垂直を確認するための補助線
- ・高さを見えるようにする線
- ・対称性を利用した線
- ・複雑な形を三角形、長方形に分ける分割線
補助線を引けるかどうかで、図形問題は難易度が大きく変わります。
次の最終章では、これらの公式を“定期テストでどう使うか”という視点で、得点力につながる実践的な攻略法をまとめていきます。
第6章|定期テストで点が取れる「公式の使い方」
頻出パターンと攻略法
定期テストで確実に点を取るために大切なのは、ただ公式を「覚える」ことではなく、どの問題で、どの公式を、どう使うか を判断できるようになることです。
数学の問題は、一見バラバラに見えても、実は いくつかのパターンに分類 できます。
この章では、その中でも テストで特に頻出の“得点源パターン” を紹介し、実際にどんな公式をどう選べばよいのかを、分かりやすく解説します。
図形問題の頻出パターン
▼面積から長さを出す問題
-
三角形の面積公式 → 底辺 or 高さを逆算
-
台形・平行四辺形も同様
-
方程式と組み合わせる問題も多い
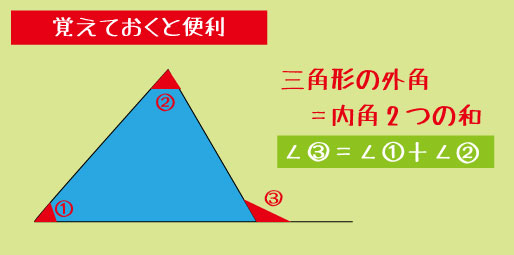
▼角度を見抜く問題
-
平行線の同位角・錯角・対頂角
-
三角形の内角・外角
-
二等辺三角形の性質
-
多角形の内角の和
▼合同・相似を使う長さ求め問題
-
合同 ⇒ 角度・辺の長さがすべて等しい
-
相似 ⇒ 比を使って長さを求める
-
特に「相似比=対応する辺の比」は定期テストで頻出
方程式の頻出パターン
▼文章題の代表パターン
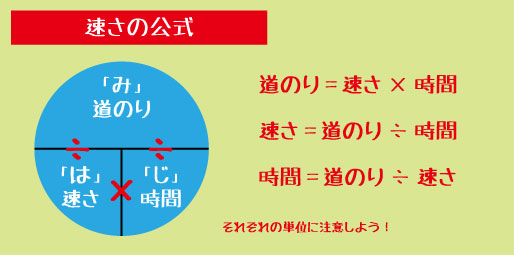
-
速さの問題(み・は・じの関係)
-
お金の問題(合計=単価×個数)
-
比例する量(値段、距離、時間など)
-
和差算の考え方が隠れていることも
▼割合・百分率の方程式
-
もとにする量 × 割合 = 比べる量
-
増減の文章題
-
食塩水の濃度(濃さ=食塩÷全体)
関数の頻出パターン
▼グラフの読み取り問題
-
y=ax(比例)
-
y=ax+b(一次関数)
-
傾きa・切片bの意味
-
点の座標を代入して式を求める
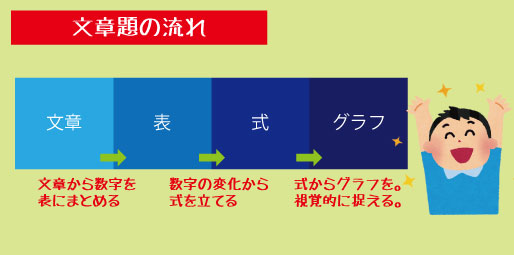
▼文章から式をつくる問題
-
「□は△の3倍」→ y=3x のように置き換える
-
「一定の量だけ増える」→ +b
-
関数の表とグラフの関係を使う
▼図形と関数の融合問題
-
三角形の面積=(底辺×高さ)÷2
-
底辺・高さが座標で求まる
-
x=0 や y=0 の交点を使う
-
「切片から求める」問題も頻出
ミスが減る「問題の見分け方」
ポイント①:まず何が“求めよ”かを確認
長さ? 面積? 時間? 金額?
→これだけで公式の候補が絞られる
ポイント②:使う公式は2〜3個しか出ない
多くの問題は
- ①図形(面積・角度・相似)
- ②方程式(文章題)
- ③関数(比例・一次関数)
のどれかに分類される。
テスト本番での攻略手順
STEP①:公式が使えそうな“合図”をチェック
-
面積 → 直角・底辺・高さ
-
相似 → 平行線・角度が等しい
-
関数 → 2点の座標が出ている
-
方程式 → 数量の関係が文章で書かれる
STEP②:図を書く(最速で点が上がる)
文章題・関数・相似は 図を描くのが最強
→ 頭の中だけで解こうとしない
STEP③:公式に当てはめるだけ
多くの問題は、「図を書く → 公式に当てはめる」の2ステップで完了。
しっかり練習すれば、テスト中に迷う時間が激減し、
確実に得点につながる“型”が身につきます!
中学数学で大切なのは、やみくもに問題を解くことではなく、学ぶ内容のつながりを理解し、「なぜその公式が必要なのか」を押さえながら学習を進めていくことです。
本コラムでは、図形・方程式・関数という中学数学の「核」になる単元を中心に、公式の成り立ちや使い方、その背後にある考え方を解説してきました。どの分野も、一見するとバラバラの内容に見えますが、実は“共通した考え方”で動いています。それは、
- 「量の関係を整理する」
- 「見えにくい部分を図や式で表す」
- 「パターン化して考える」
という3つの力です。この3つを身につければ、どの単元でもスムーズに理解が進み、定期テストでも安定して点が取れるようになります。
図形の学習では、角度の性質や面積の公式、合同・相似など、図を使った理解がとても重要でした。特に、図を自分で描く習慣がつくと、問題の見通しが一気に良くなり、解法がシンプルにまとまります。
方程式では、「文章を式に置き換える力」がポイントでした。実際、文章題は複雑に見えても、数量の関係を図や表で整理すればほとんどが同じパターンに落ち着きます。
そして関数では、比例・一次関数・グラフの読み取りなど、日常生活の中にもつながる“変化を読み取る力”が問われました。点の座標、傾き、切片といった要素も、ルールさえ理解すればとても扱いやすくなります。
また最終章では「公式をいつ使うか」という実戦的な視点から、頻出パターンと攻略法を紹介しました。特にテスト本番では、公式を暗記しているだけでは点は伸びません。問題文のどこにヒントが隠れているのか、どの公式が当てはまりそうか、どの順番で処理すべきか。こうした判断力は、練習を重ねることで必ず鍛えられます。大事なのは、ミスを怖がらず、1つずつ自分のペースで積み上げることです。
勉強は、誰かと比べる必要はありません。昨日の自分より、今日の自分が少しでも「できること」が増えたなら、それが確かな成長です。このコラムで整理した公式や考え方を、あなたのペースで何度も復習してみてください。最初は難しく感じた公式も、何度か使っているうちに自然と手になじみ、自信につながっていきます。
数学は“積み重ね”の教科ですが、
同時に、“気づいた瞬間に
一気に理解が深まる教科”でもあります。
あなたがこれから取り組む勉強が、無理なく続けられ、努力がしっかり結果につながることを願っています。小さな一歩の積み重ねが、必ず大きな力になります。焦らず、自分を信じて、一緒にがんばっていきましょう。
応援しています!
お子さまの学習にお悩みの保護者の方へ。

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ!!
こちら各種SNSでも情報配信中です。参考にしてみてください。
/
この記事は 1,633人 に閲覧されています。
.jpg)




なぜ「公式を覚えるだけ」では点が取れないのか
公式を丸暗記しているだけだと、実践問題で必ずつまずきます。
たとえば、三角形の面積公式を知っていても「どれが高さなのか」が分からなければ計算できませんし、一次関数の式を覚えていても「傾きの意味」が理解できていなければ文章題に太刀打ちできません。
公式は“使う道具”であり、使い方を知らなければ宝の持ち腐れになってしまいます。定期テストでは単純な暗記問題は少なく、「公式の意味を理解し、正しく選ぶ問題」が多数出題されます。
だからこそ、“暗記”ではなく“理解と判断”が大切なのです。