一次関数「変域」が苦手な中学生へ 定期テスト・高校受験での得点アップにつながるグラフ思考
中学数学の中でも「一次関数の変域」は、多くの中学生がつまずきやすい単元のひとつです。
一次関数そのものは「y＝ax＋b」というシンプルな式ですが、そこに「変域（xやyが取りうる値の範囲）」が加わると、一気に難しく感じてしまう人が少なくありません。グラフを使えばイメージしやすいはずなのに、計算だけで処理しようとして混乱してしまった経験はないでしょうか。
では、どうすれば「変域」を得意分野にできるのでしょうか。
ポイントは “グラフで考える習慣” を身につけることです。
式を見ただけで処理しようとせず、一度グラフに描いて「xが動けばyはどう変わるか」を視覚的にとらえることで、正しい答えにたどり着きやすくなります。また、傾きが負のときの大小関係の逆転といった“ひっかけ”も、グラフを描けば自然に理解できます。
このコラムでは、一次関数の基本から始めて、「変域」の定義・計算方法・注意点、さらに定期テストや高校入試に出やすい応用問題までを体系的に整理します。最後には、得点アップにつながる学習法も紹介するので、苦手意識を克服したい人や受験対策を万全にしたい人にとって、きっと役立つはずです。
第1章 一次関数の基本をおさらい
一次関数とは？
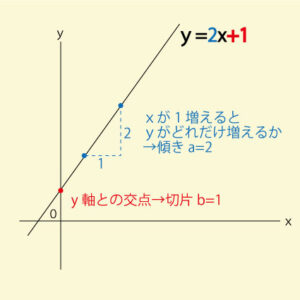
一次関数とは、変数xに比例して値が変化する関数で、一般的に「y＝ax＋b」という形で表されます。ここで、aは「傾き」、bは「切片」と呼ばれます。
- 傾き：xが1増えると、yがどれだけ増減するかを表す値
- 切片：直線がy軸と交わる点のこと
aとbが決まれば、グラフはただ一つに定まります。
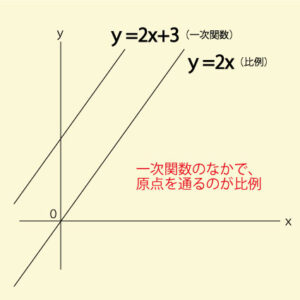
比例との違いを理解しよう
中1で学習する「比例 y＝ax」と、一次関数はよく似ています。しかし、比例では必ず原点（0,0）を通るのに対して、一次関数は切片bの値によって、グラフが上下にずれるのが大きな違いです。
この「bの存在」により、日常生活のさまざまな場面をモデル化できるのが一次関数の強みです。例えば「タクシー料金＝初乗り料金＋距離に応じた料金」のような関係は、まさに一次関数で表せます。
一次関数とグラフの関係
一次関数の式は、必ず直線としてグラフに表せます。xにいくつかの値を代入してyを計算し、その点をプロットしていけば、直線が引けるはずです。
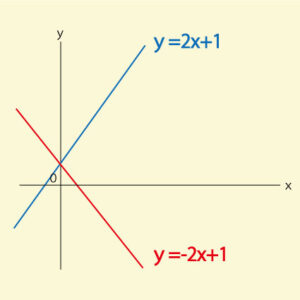
特に「傾きaの符号」に注目すると、グラフの向きが分かりやすくなります。
- aが正 → 右上がりの直線
- aが負 → 右下がりの直線
このルールを覚えておくと、式を見ただけでグラフの大まかな形をイメージできるようになります。
第2章 「変域」とは？
一次関数の学習でよく出てくるキーワードが「変域」です。式そのものは理解できても、
「変域って何？」
「どうやって読み取ればいいの？」
と混乱する中学生は多いものです。定期テストや入試の問題でも「xの変域が与えられているとき、yの変域を答えなさい」という形式は頻出です。まずは、変域の意味を正しく理解し、グラフとセットでイメージできるようにしましょう。
変域の定義をおさえよう
変域とは、変数が取りうる値の範囲を指します。
一次関数の場合、主に「xの変域（xの範囲）」と「yの変域（yの範囲）」が登場します。
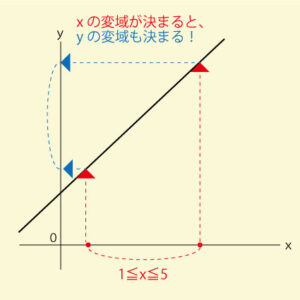
たとえば「1≦x≦5」と書かれていれば、xは1から5までの値を動く、という意味になります。そして、その範囲のxを代入して得られるyの範囲が「yの変域」です。つまり、xの範囲が決まるとyの範囲も決まるのです。
グラフで考えると理解しやすい
変域を理解する最大のコツは「グラフで考えること」です。
式だけで処理しようとすると、xを代入して計算し、最小値と最大値を比較する手間がかかります。しかし、グラフを描けば「xがこの範囲を動くとき、直線上の点はどこからどこまで動くか」が一目で分かります。特に、yの最小値・最大値を考えるとき、グラフの両端の点を確認するだけで済むのです。
日常生活での変域のイメージ
変域は単なる計算用語ではなく、身近な場面でも活用できます。
例えば「1時間で時速60kmで走る車の位置」を一次関数で表すと、xを「時間」、yを「距離」とすれば、0≦x≦1のとき、0≦y≦60 となります。
このように、変域は「状況の制約を表すもの」として考えると分かりやすいのです。入試問題でも「水を入れる」「物を動かす」といった具体的な状況設定がよく登場します。
第3章 変域の求め方
変域の学習で最もよく出題されるのが「xの範囲が与えられているときに、yの範囲を求める問題」です。式を正しく扱えば決して難しくはありませんが、計算の流れをつかんでいないと混乱しやすい単元です。ここでは、基本的な手順を整理しながら、例題を使って実際に解き方を確認していきましょう。
基本の手順を確認しよう
一次関数 y＝ax＋b のとき、xの範囲が与えられたら次の手順でyの変域を求めます。
- 与えられたxの最小値と最大値を式に代入する
- それぞれのyの値を計算する
- 得られたyの小さい方が最小値、大きい方が最大値
この流れを覚えておけば、ほとんどの問題に対応できます。
解き方
- x＝0 を代入 → y＝2×0＋3＝3
- x＝4 を代入 → y＝2×4＋3＝11
- よって、yの変域は 3≦y≦11 となります。
このように「両端の値を代入して比べる」だけで答えが出ます。傾きが正の場合は、xの増加に伴ってyも増えるため、自然と小さい方が最小値、大きい方が最大値になります。
計算の確認ポイント
計算自体はシンプルですが、見落としがちなポイントもあります。
- 両端のxを必ず確認すること：途中の値を考える必要はなく、端点だけでOK
- 整数に限らない：変域は「範囲」を表すので、途中に小数や分数の値も含む
- 不等号の向きをそのまま残す：求めた範囲は「◯≦y≦◯」の形にするのが基本。
このルールを守れば、テストでの計算ミスをぐっと減らせます。
第4章 変域の注意ポイント！
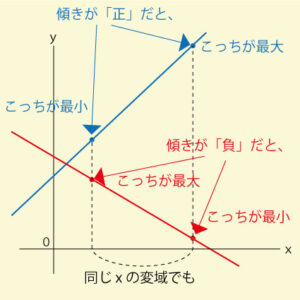
一次関数の変域の問題で、もっとも間違えやすいケースが「傾きが負」の場合です。
傾きが正のときは「xが増えるとyも増える」ため直感的に理解しやすいのですが、傾きが負になると「xが増えるとyは減る」という逆の動きになります。ここで大小関係を取り違えると、答えが逆になってしまうのです。テストや入試ではこの“逆転”を意識できるかどうかが得点の分かれ目になります。
傾きが負のときに起こること
一次関数 y＝ax＋b で a＜0 の場合、グラフは右下がりの直線になります。つまり、xが大きくなるにつれて、yの値は小さくなっていくのです。そのため「xの最小値を代入したときのy」が最大値、「xの最大値を代入したときのy」が最小値になる、という逆転現象が起こります。
例題で確認しよう
例題
一次関数 y＝−2x＋6 のとき、0≦x≦3 の範囲で y の変域を求めなさい。
解き方
- x＝0 を代入 → y＝−2×0＋6＝6
- x＝3 を代入 → y＝−2×3＋6＝0
- 傾きが負なので「xが小さいときにyは大きく、xが大きいときにyは小さくなる」。
→ よって y の変域は 0≦y≦6 となります。
多くの生徒が「6≦y≦0」と書いてしまいがちですが、不等号の向きを正しく書くことが大切です。
ミスを防ぐコツ
傾きが負のときの変域でミスを防ぐためには、以下の工夫が役立ちます。
- 必ずグラフを描く：頭の中だけで考えるより、直線を描いた方が確実。
- 両端のxを代入して比べる：計算結果を並べて「どちらが大きいか」を確認する。
- 不等号は必ず「小さい値≦y≦大きい値」に並べる：数値の大小関係を整理してから書く習慣をつける。
これらを意識するだけで、傾きが負の問題でも安心して解けるようになります。
第5章 「変域」の出題パターン
一次関数の「変域」は、多くの中学生が定期テストで苦戦するポイントの一つです。グラフの基礎を理解していても、「数値条件を満たす範囲をどのように読み取るか」で混乱しがちです。
しかし、出題されるパターンにはある程度の「型」が存在します。この章では、よく出題される3つの代表的なパターンを整理し、それぞれの解き方のコツを紹介します。
xの範囲が指定されている問題
もっとも基本的なのは、「xの範囲を指定し、そのときのyの範囲を求める」問題です。
【例題】関数 y=2x−1において、1,≦x≦4 のとき、yの変域を求めよ。
【解き方の流れ】
-
１）区間の両端（x=1とx=4）を代入する。
- x=1 → y=2×1-1=1
- x=4 → y=2×4-1=7
-
２）増加関数（a>0）なので、小さい方が最小値、大きい方が最大値。
→ よって yの変域は「1 ≦ y ≦ 7」となる。
xの範囲を逆に問う問題
テストでは「yの範囲が与えられたとき、xの範囲を答える」逆の出題もあります。
【例題】関数 y=−x+3 において、1≦y≦4 のとき、xの範囲を求めよ。
【解き方の流れ】
-
１）端の値を使って、逆にxを解く。
- y=1 → 1=-x+3 x=3-1=2
- y=4 → 4=-x+3 x=3-4=-1
-
２）減少関数（a<0）の場合は、大小関係に注意。
→ y=1のときx=2が右端、y=4のときx=-1が左端。
→ よって xの範囲は「-1 ≦ x ≦ 2」となる。
応用問題（図形との組み合わせ）
発展的には、一次関数の変域が「図形の条件」と組み合わさって出題されます。
【例題】一次関数 y=1/2x のグラフについて、点A(0,0)から点B(6,3)までの部分を考える。このときのyの変域を求めよ。
【解き方の流れ】
-
１）区間の両端AとBを確認。
- x=0 → y=1/2×0=0
- x=6 → y=1/2×6=3
-
２）グラフは直線で連続するので、yの範囲は「0 ≦y ≦ 3」。
第6章 実践的な勉強法と心構え
一次関数の「変域」は、ただ知識を暗記するだけでは解けないことが多い分野です。グラフを描き、数直線を意識し、文章を数式に変換する「考える力」が求められます。テストや入試本番で得点するためには、日頃の学習の工夫と試験当日の心構えが大切です。ここでは、効果的な勉強法と、最後に意識してほしいポイントを整理していきましょう。
毎日少しずつ
一次関数の問題は、頭の中だけで処理しようとすると混乱しやすくなります。だからこそ、必ず紙にグラフを描いて確認する習慣をつけましょう。
- 与えられた式から傾きと切片を確認する
- 変域をもとに、始点と終点を打ってグラフを描く
- 求めたい値をグラフから視覚的に読み取る
この3ステップを毎日繰り返すことで、「頭でイメージする → 手を動かす → 確認する」という一連の流れが自然にできるようになります。
典型問題を繰り返して「型」を身につける
一次関数の変域の出題は、パターンが限られています。
たとえば：
- グラフから値を読み取る問題
- 変域に対応する値の範囲を求める問題
- 文章題を数式に変換して解く問題
これらのパターンを意識しながら、学校や塾の問題集で繰り返し練習することで「どのアプローチを使えばいいか」がすぐに判断できるようになります。特に入試直前期には「問題を見て、すぐに型を思い出す」ことができるかどうかが得点の分かれ目になります。
試験本番の時間配分と心構え
テストや入試では、時間に追われる中で冷静さが求められます。以下の流れを意識してみてください。
- まずはグラフを描く（焦らずに丁寧に）
- わかる部分から答える（難問に時間を取られすぎない）
- 見直しの時間を確保する（符号や範囲の書き間違いが多いため要注意）
また、「変域」の問題は、図を描くかどうかで正答率が大きく変わります。頭の中だけで処理せず、必ず「目で確認する」ことを試験中でも意識しましょう。
一次関数の変域は、「公式を覚える」だけでは対応しきれない分野です。
- １）日々の学習でグラフを描く習慣を身につける
- ２）典型問題の「型」をストックする
- ３）試験本番では冷静に処理すること
この3点を意識すれば、得点力は確実に上がります。高校受験は「自分の努力が数字として結果に出る」大きなチャンスです。変域の問題をマスターし、数学の得点アップを実感することで、自信を持って入試本番に臨みましょう。
一次関数の「変域」を理解すれば数学が味方になる！
ここまで、一次関数の基本から「変域」の考え方、そして定期テストや高校受験につながる具体的な活用法までを見てきました。一次関数は中学数学の中でも大きな山場となる単元であり、特に「変域」に関する理解は得点力に直結します。最初は抽象的に感じられるかもしれませんが、グラフを用いて整理したり、実際の問題を解きながら確認したりすることで、少しずつ自分のものにできるはずです。
変域は単なる数値の範囲ではなく、「入力と出力の関係を限定するルール」だと考えると、理解がぐっと深まります。この視点を持てば、応用問題や文章題に直面しても、落ち着いて条件を整理し、正確に解答へつなげられるようになります。つまり、変域を制することは、一次関数そのものを自在に使いこなす第一歩なのです。
また、テスト勉強や受験対策においては「典型パターンの問題」を解くだけでなく、自分でグラフを書いて確認する学習法が有効です。頭の中でイメージするよりも、手を動かして目で確かめることで、理解の定着は格段に早まります。さらに、間違えた問題を「なぜそうなるのか」と振り返る習慣をつければ、弱点が確実に克服されていきます。
お子さまの学習にお悩みの保護者の方へ。
当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。
※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。
お気軽にどうぞ！！
こちら各種SNSでも情報配信中です。参考にしてみてください。
/
この記事は 20人 に閲覧されています。
オススメコラム
【２０２２年７月度】目指せ！自分史上最高の夏休み♪夏の新規入会キャンペーン実施中！！
目次２０２２年７月度新規入会キャンペーンを実施します。特典１ 入会金 無料特典２ 初月通常指導料 無料特典３ 夏期講習1教科 無料 目指せ！！自分史上最高の夏休み♪ ２０２２年７月度 新規入会キャンペーン […]
堺市北区の北長尾町に新規開校！【個別学習指導イマナビ：堺長尾教室】
目次■ 堺市北区北長尾町に新規開校 ■■ イマナビって？？ ■・徹底個別 ・家庭学習指導 ■ どんな生徒に合ってるの？ ■■ 無料個別相談会 ■ ■ 堺市北区北長尾町に新規開校 ■ 堺の東の玄関口と位置付け […]
小学生の算数苦手を克服！つまづきやすい単元とその克服法を知ろう
算数は、小学生にとって重要な学びの基盤となる教科ですが、多くの子どもたちが特定の単元でつまづくことがあります。算数の苦手意識は早期に対処することが大切です。 目次算数のつまづきやすい単元と克服法１．つまづき […]
例題で実際に解いてみよう
例題
一次関数 y＝2x＋3 のとき、0≦x≦4 の範囲で y の変域を求めなさい。