文章題・速さ・割合が一気に楽になる！小学生から中学生までの「単位量当たりの大きさ」徹底ガイド

「文章題が苦手」
「速さや割合になると急に分からなくなる」

これは、小学生・中学生、そして保護者の方から非常によく聞く悩みです。計算練習はそれなりにできているのに、文章題になると式が立てられない。速さや割合の単元に入った途端、テストの点数が下がってしまった——そんな経験はありませんか。

実は、こうしたつまずきの多くは「計算力不足」や「努力不足」が原因ではありません。その背景には、「単位量当たりの大きさ」という考え方が十分に身についていないという共通点があります。

「単位量当たりの大きさ」と聞くと、難しそうな言葉に感じるかもしれません。しかし、その正体はとても身近なものです。たとえば、「1個あたりの値段」「1時間あたりに進む距離」「1人分に分けたときの量」など、私たちは日常生活の中で無意識にこの考え方を使っています。算数では、これを意識的に使いこなせるようになることが求められているのです。

ところが、多くの子どもたちは「割り算＝計算」として覚えてしまい、「比べるために1あたりを考える」という本来の意味を十分に理解しないまま学年が進んでしまいます。その結果、文章題になると「何を求めればいいのか分からない」、速さや割合になると「公式は覚えたけれど使い分けられない」という状態に陥ってしまうのです。

特に重要なのは、速さ・割合・平均は、すべて「単位量当たりの大きさ」という同じ考え方でつながっているという点です。速さは「1時間あたりの距離」、割合は「もとにする量を1としたときの大きさ」、平均は「全体を同じ大きさに分けた1つ分」。形は違っても、考え方の根っこは同じなのです。

この共通構造を理解できている子は、文章題や応用問題にも強くなります。一方で、ここが曖昧なままだと、小学校高学年から中学校にかけて、算数・数学が一気に難しく感じられるようになります。中学数学で登場する比例・反比例、関数、グラフの読み取りなども、実はすべて「単位量当たりの大きさ」の理解が土台になっています。

だからこそ、この考え方は「一つの単元」ではなく、算数・数学全体を支える重要な土台だと言えるのです。

本コラムでは、小学生から中学生までを対象に、「単位量当たりの大きさ」を基礎から丁寧に解説します。なぜ文章題が苦手になるのか、速さや割合がどうつながっているのか、そして、どのように考えれば理解が深まるのかを、具体例や図解を交えながら分かりやすく紹介していきます。

「算数・数学が苦手かもしれない」と感じている子どもたち、そしてその成長を支えたい保護者の方にとって、このコラムが“つまずきの正体”を知るきっかけとなり、「分かる」への第一歩になることを願っています。

第1章：そもそも「単位量当たりの大きさ」とは何か？
第2章：文章題が苦手になる本当の原因は「式」ではない
第3章：速さ・割合・平均はすべて同じ考え方
第4章：小学生で必ず身につけたい3つの考え方
第5章：中学生で差がつく「単位量当たり」の応用力
第6章：単位量当たりの理解が、算数・数学を得意にする

第1章：そもそも「単位量当たりの大きさ」とは何か？

― 小学生が最初につまずきやすい理由 ―

算数の学習が進むにつれて、

「計算はできるのに文章題になると分からない」
「割り算の意味がよく分からないまま進んでいる気がする」

と感じる子どもは少なくありません。特に小学校高学年になると、その傾向はよりはっきりと表れてきます。その背景にある重要なキーワードが、「単位量当たりの大きさ」です。

この言葉自体は少し難しく聞こえますが、実は算数が苦手になるかどうかの分かれ道とも言える、とても大切な考え方です。ここを正しく理解できているかどうかで、文章題や応用問題への取り組みやすさが大きく変わってきます。

単位量当たりの大きさとは「1あたり」で比べること

「単位量当たりの大きさ」とは、簡単に言えば、

「1あたりの量にそろえて比べる考え方」

のことです。

「1個あたり」「1つ分」「1kmあたり」「1時間あたり」など、必ず「1」が基準になります。

たとえば、10個で500円のお菓子と、8個で480円のお菓子があったとします。合計金額だけを見ると前者の方が高く見えますが、「1個あたりの値段」で比べるとどうでしょうか。

500円 ÷ 10個＝ 1個あたり50円

480円 ÷ 8個＝ 1個あたり60円

このように、「1個あたり」に直すことで、どちらが本当にお得なのかがはっきりします。

実は身の回りにあふれている「単位量当たり」

単位量当たりの考え方は、算数の問題の中だけに存在するものではありません。私たちは日常生活の中で、自然にこの考え方を使っています。

・1個あたりの値段
スーパーで商品を選ぶとき、「たくさん入っていて安いかどうか」を無意識に比べています。

・1mあたりの長さ・値段
布やロープを買うとき、長さあたりの価格を見て判断します。

・1時間あたりの速さ
車や電車の速さは、「1時間にどれくらい進むか」で表されます。

これらはすべて、「量をそろえて比べる」ために単位量当たりに直している例です。算数の問題は、実はこうした日常の判断を、数字と式で表しているだけなのです。

なぜ小学生は「割り算＝計算」だと思ってしまうのか

多くの小学生は、割り算を「答えを出すための計算」として覚えがちです。「とにかく割ればいい」「式を立てればいい」と考えてしまい、その意味まで意識できていないケースが少なくありません。

しかし、本来の割り算は「分ける」「1あたりを求める」ためのものです。この意味が理解できていないと、文章題で「何を割ればいいのか」が分からなくなります。結果として、数字は読めているのに、式が立てられないという状態に陥ってしまうのです。

文章題が急に難しく感じられるのは、計算が難しくなったからではありません。

「比べるために1あたりを考える」という視点が

抜け落ちてしまっていることが、大きな原因なのです。

単位量当たりの大きさは、特別なテクニックではなく、「比べるための考え方」です。この考え方が身につくと、文章題の読み取りが楽になり、「何を求めればいいのか」が自然と見えるようになります。小学生が最初につまずきやすいのは、能力の問題ではなく、この視点にまだ慣れていないだけなのです。

次章では、文章題が苦手になる本当の原因をさらに掘り下げ、「どこで読み違えてしまうのか」を具体的に見ていきます。

第2章：文章題が苦手になる本当の原因は「式」ではない

― 読み取れないのはどこか？ ―

文章題が苦手な子に理由を聞くと、

「式が分からない」
「どんな計算をすればいいか分からない」

という答えが返ってくることがよくあります。しかし、実際の学習現場を見ていると、問題は式以前の段階にあるケースがほとんどです。

多くの子どもたちは、文章題を「計算問題」として捉えすぎています。その結果、数字だけを追いかけてしまい、「何について比べているのか」「何を求める問題なのか」を十分に考えないまま式を立てようとしてしまうのです。ここに、文章題が急に難しく感じられる本当の原因があります。

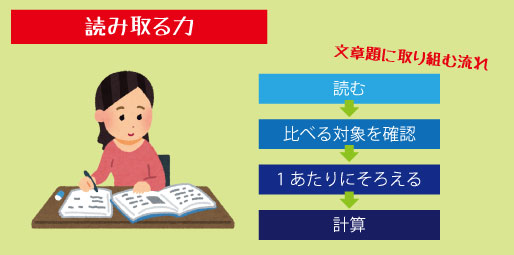
文章題で本当に必要なのは「読み取る力」

文章題を解くために必要なのは、計算力だけではありません。大切なのは、次の2つの力です。

数字を正しく読む力
どの数字が「全体」で、どの数字が「比べるための材料」なのかを見分ける力。

「何を比べているか」を見抜く力
合計を比べたいのか、それとも1あたりを比べたいのかを判断する力。

たとえば、「どちらが安いですか」と書かれていても、実際に比べるべきなのは合計金額ではなく、「1個あたりの値段」であることが多くあります。この判断ができないと、正しい計算をしていても答えがずれてしまうのです。

単位量当たりを見抜けない典型的な文章題

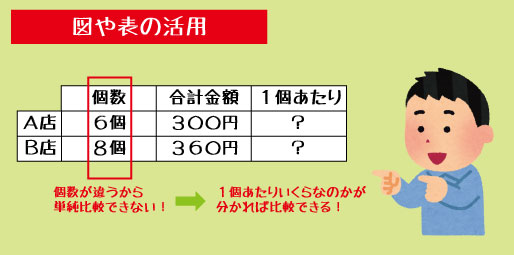
文章題でよくあるつまずきの例として、「お店の値段比較」があります。

A店では6個で300円、B店では8個で360円の商品が売られているとします。

このとき、「どちらの店の方が安いでしょうか」

この問題を見て、合計金額だけを比べてしまう子は少なくありません。しかし、この問題で本当に比べたいのは、「1個あたりの値段」です。

同じように、人数が違うクラスの平均を比べる問題も典型例です。

Aクラスは20人で合計点数が1400点

Bクラスは25人で合計点数が1600点

どちらのクラスの平均点が高いか

と聞かれたとき、合計点数だけを見てしまうと正しい判断ができません。

これらの問題に共通しているのは、

「どちらが多いか」ではなく、「どちらが1あたり大きいか」

を考える必要がある点です。

図や表にすると、文章題は一気に分かりやすくなる

文章題が苦手な子ほど、頭の中だけで考えようとしてしまいます。しかし、単位量当たりの問題は、図や表に整理することで一気に見えるようになる特徴があります。

たとえば、店の値段比較なら「個数」「合計金額」「1個あたり」の3つを表にするだけで、どこを比べればよいのかが明確になります。人数が違う平均の問題でも、「人数」と「合計」を並べて書くだけで、「1人あたり」を求める必要があることが自然と分かります。

図や表は、答えを出すための近道ではありません。

「何を比べる問題なのか」を自分で理解するための大切な手段なのです。

文章題が苦手になる原因は、計算ができないことではなく、「何を比べる問題なのか」を読み取れないことにあります。「どちらが多い？」ではなく、「どちらが1あたり大きい？」という視点を持つことで、文章題の見え方は大きく変わります。

次章では、この「単位量当たりの考え方」が、速さ・割合・平均とどのようにつながっているのかを解説し、算数から中学数学への橋渡しをしていきます。

第3章：速さ・割合・平均はすべて同じ考え方

― 中学数学につながる超重要ポイント ―

速さ、割合、平均。

これらの単元を聞いたとき、「それぞれ別の公式を覚えるもの」「単元ごとに考え方が違う」と感じている子どもは少なくありません。実際、小学校でもこれらは別々の単元として扱われるため、つながりを意識する機会はあまり多くないのが現状です。

しかし実は、この3つはまったく別の考え方ではありません。すべてに共通しているのが「単位量当たりの大きさ」という考え方です。この共通点に気づけるかどうかが、算数を「理解する教科」にできるかどうか、そして中学数学で伸びるかどうかの大きな分かれ道になります。

速さは「1時間あたり」にそろえて考える

速さとは、「どれくらい速いか」を表す量ですが、その正体はとてもシンプルです。

速さ＝1時間あたりに進む距離。

つまり、「時間を1にそろえて比べる」単位量当たりの考え方そのものなのです。

たとえば、Aさんは2時間で10km、Bさんは3時間で15km進んだとします。

合計の距離だけを見ると、どちらも同じように見えますが、

「1時間あたり」に直すと、

Aさん：10km ÷ 2時間＝ 5km/時間

Bさん：15km ÷ 3時間＝ 5km/時間

となり、同じ速さだと分かります。

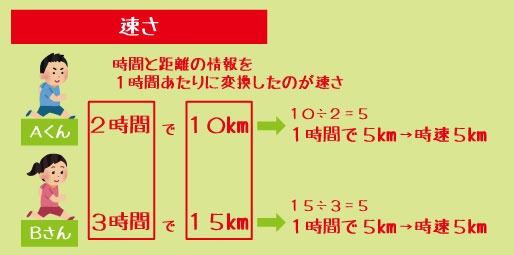
速さの問題が苦手な子は、「距離÷時間」という式だけを覚えています。しかし本当に大切なのは、「時間を1にそろえて比べている」という意味を理解することです。

割合と平均も、考え方はまったく同じ

割合もまた、「もとにする量を1としたときの大きさ」を表しています。

たとえば、全体が100で、そのうち20であれば、割合は0.2（20％）です。これは、「全体を1としたとき、その部分はどれくらいか」を見ているだけなのです。

平均も同様です。平均とは、全体を同じ大きさに分けたときの1つ分。合計を人数で割るのは、「1人あたり」にそろえるための操作です。

・速さ：1時間あたり
・割合：もとにする量を1としたとき
・平均：1つ分に分けたとき

表現は違っても、すべて「基準を1にそろえて比べる」という単位量当たりの考え方で統一されています。

この理解が中学数学で大きな差を生む

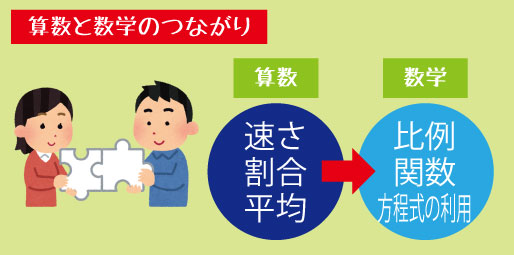
単位量当たりの理解がしっかりしている子は、中学数学に入ってから大きく伸びます。なぜなら、中学数学で扱う「比例」「反比例」「関数」「変化の割合」は、すべてこの考え方を土台にしているからです。

たとえば、グラフの傾きは「xが1増えたときに、yがどれだけ増えるか」、つまり単位量当たりの変化量です。この意味が分かっていないと、公式は覚えても応用ができません。一方で、小学校のうちから「1あたり」を意識できている子は、数式やグラフを自然に理解できるようになります。

算数と数学の間にある見えない壁は、計算の難しさではなく、考え方の切り替えにあります。その橋渡しをしてくれるのが、単位量当たりの大きさなのです。

速さ・割合・平均は、別々の単元ではなく、すべて「単位量当たりの大きさ」という1つの考え方で結ばれています。この共通点に気づくことで、算数は暗記科目から「理解する教科」へと変わります。

次章では、小学生のうちにぜひ身につけておきたい、単位量当たりを理解するための具体的な考え方や学習のポイントを紹介していきます。

第4章：小学生で必ず身につけたい3つの考え方

― 計算よりも大切なこと ―

算数が得意な子と、だんだん苦手になっていく子。その差は、計算スピードや暗記量ではありません。特に小学校高学年（小5・小6）になると、「学校のテストではそれなりに点が取れるのに、少しひねった問題や文章題になると急に崩れる」というケースが目立ってきます。

その原因は、計算技術の不足ではなく、考え方の土台が十分に育っていないことにあります。単位量当たりの大きさを正しく理解するために、小学生のうちにぜひ身につけておきたい考え方が、ここで紹介する3つです。

「何を1とするのか」を意識できているか

単位量当たりの問題で最も重要なのは、

「何を1として考える問題なのか」

を意識することです。

1個なのか、1人なのか、1時間なのか、1mなのか。この基準があいまいなまま計算を始めると、答えが合っていても理解は深まりません。

小学生の多くは、「割る」という操作には慣れていますが、

「なぜ割るのか」
「何を1にそろえたいのか」

を考える習慣がまだ十分ではありません。そのため、問題文の中で基準が少し変わると、急に混乱してしまいます。

いきなり式を立てず、言葉で説明できるか

算数が得意な子ほど、実は「式を書く前」に考えています。一方で、つまずきやすい子は、問題を読んだ瞬間に数字を拾い、すぐに式を作ろうとします。

ここで大切なのが、

「この問題は何を比べたいのか」

「まず何を求める必要があるのか」

を、言葉で説明できるか

という点です。

たとえば、「1個あたりの値段を出してから比べる」「1人あたりに直して考える」と言えるかどうか。この一言が言えるだけで、式の意味がはっきりします。

言葉で説明できないまま立てた式は、応用がききません。数字が変わったり、聞かれ方が変わったりすると、一気に手が止まってしまいます。

図・表・線分図に表す習慣が応用力を育てる

単位量当たりの考え方は、頭の中だけで処理しようとすると難しく感じます。しかし、図や表に表すことで、驚くほど整理されます。

特に効果的なのが、

・表（合計量／単位量）
・線分図（量の関係を視覚化）

です。

小5・小6になると、「図を書くのは面倒」「早く計算したい」と図を省略しがちになりますが、ここで図を描く習慣があるかどうかが、中学以降の数学力に直結します。

学校のテストで点が取れていても、応用問題で崩れる子は、考え方を支える“見える道具”を持っていないことが多いのです。

家庭学習で意識したい声かけのポイント

家庭での関わり方も、考え方の定着に大きく影響します。

おすすめなのは、次のような声かけです。

「何を1として考えてる？」

「いきなり計算しなくていいよ。まずどう考える？」

「図にするとどうなるかな？」

「早くしなさい」「計算合ってる？」ではなく、「考え方」に目を向けた声かけをすることで、子どもは少しずつ“理解する算数”へと変わっていきます。

単位量当たりの大きさを理解するために必要なのは、難しい計算力ではありません。「何を1とするか」「言葉で考える」「図や表で整理する」。この3つの考え方が身についていれば、算数は確実に安定していきます。

次章では、この力が中学生になるとどのように活かされ、どこで差がつくのかを、より具体的に見ていきます。

第5章：中学生で差がつく「単位量当たり」の応用力

― 比例・反比例・関数へのつながり ―

中学生になると、「数学が急に難しくなった」と感じる生徒が一気に増えます。比例・反比例、関数、グラフ、文章題——どれも計算そのものが極端に難しくなるわけではありません。それでも点数に差がつくのは、考え方の土台があるかどうかが問われるようになるからです。

この土台の中心にあるのが、「単位量当たりの大きさ」の理解です。小学生のうちにこの考え方が身についているかどうかで、中学数学の見え方は大きく変わります。

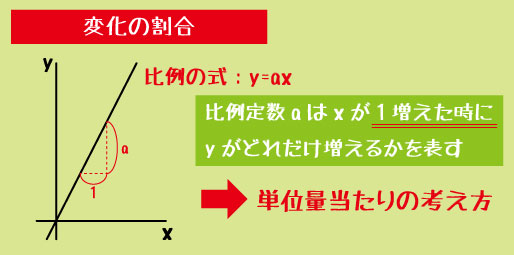
「変化の割合」は単位量当たりの大きさそのもの

中学数学で登場する重要な概念に、「変化の割合」があります。

これは、「xが1増えたときに、yがどれだけ変わるか」という量です。

つまり、変化の割合とは

「1あたりの変化量」＝単位量当たりの大きさ

にほかなりません。

比例の式「における「a」は、xが1増えたときにyがどれだけ増えるかを表しています。これは、小学校で学んだ「1個あたりの値段」や「1時間あたりの速さ」と、考え方としてはまったく同じです。

グラフの傾きが分からない理由

中学生がつまずきやすいポイントの一つが、「グラフの傾き」です。

多くの生徒は、傾きを「公式で求めるもの」として覚えていますが、その意味を十分に理解していません。

グラフの傾きとは、「横に1進んだとき、縦にどれだけ変わるか」。

これもまた、単位量当たりの考え方です。

この意味が分かっていないと、

グラフを見ても何を表しているか分からない
文章題とグラフが結びつかない
速さ・割合・関数が別物に見える

といった状態になりがちです。一方で、「1あたり」という視点が身についている生徒は、グラフを“形”ではなく“意味”として読むことができます。

文章題・関数問題でよくある失敗例

中学数学の文章題でよく見られる失敗は、「式は立てられているのに、考え方がズレている」ケースです。

たとえば、速さの文章題で「距離÷時間」は書けているものの、「何を1として比べているのか」が分かっていないため、条件が少し変わると対応できなくなります。

比例・反比例の文章題でも、「比例だからこの式」「反比例だからこの式」と暗記で処理してしまうと、応用問題で必ず壁にぶつかります。

大切なのは、

「1あたりにそろえると、どんな関係が見えるか」

を考えることです。

小学生のうちに理解していると圧倒的に有利な理由

小学生のうちに単位量当たりの大きさを理解している子は、中学数学で次のような強みを持ちます。

・新しい単元でも「考え方の軸」がブレない
・文章題を読んだ瞬間に「何を1にするか」を判断できる
・公式を覚えなくても、自分で意味から作れる

結果として、「暗記数学」ではなく「理解する数学」に自然と移行できます。これは、定期テストだけでなく、高校数学やその先の学習にも大きく影響します。

中学数学で差がつく最大のポイントは、計算力や暗記量ではありません。「単位量当たりの大きさ」という考え方を土台に、比例・反比例・関数・文章題を一本の線でつなげて理解できるかどうかです。

次章では、この考え方が算数・数学全体をどのように支え、これから学ぶ子・つまずいている子にとってどんな意味を持つのかをまとめていきます。

第6章：単位量当たりの理解が、算数・数学を得意にする

― これから学ぶ子・つまずいている子へ ―

算数や数学が苦手だと感じている子どもたちの多くは、「自分は向いていない」「センスがない」と思い込んでしまいがちです。しかし、これまで見てきたように、つまずきの原因は能力や努力不足ではありません。多くの場合、考え方の土台がまだ十分に整っていないだけなのです。

その土台の中心にあるのが、「単位量当たりの大きさ」という考え方です。この考え方を理解できるかどうかで、算数・数学の見え方は大きく変わります。

単位量当たりは「一生使う考え方」

単位量当たりの大きさは、小学校や中学校だけで使う特別な知識ではありません。

買い物、移動、時間管理、データの比較など、私たちの生活は「1あたりで考える」場面にあふれています。

算数・数学の学習は、こうした現実の判断力を育てるトレーニングでもあります。単位量当たりを理解することは、「計算ができるようになる」だけでなく、「物事を正しく比べ、考える力」を身につけることにつながります。

つまずいている今こそ、見直す価値がある

もし今、文章題や速さ、割合でつまずいていたとしても、決して遅すぎることはありません。むしろ、「分からない」と感じている今こそ、単位量当たりの考え方を見直す絶好のタイミングです。

計算練習を増やすよりも、

・何を1として考える問題なのか
・何を比べたいのか

を丁寧に確認することで、理解は一気に進みます。

多くの子どもは、ここが整理されるだけで「急に分かるようになった」と感じます。それは、点だった知識が線でつながる瞬間でもあります。

「できない」は「まだ整理できていない」だけ

算数・数学に苦手意識を持つ子ほど、「間違えたらどうしよう」「自信がない」という気持ちを抱えています。しかし、単位量当たりの視点で考えられるようになると、問題に対する向き合い方が変わります。

いきなり答えを出そうとせず、

「これは1あたりを考える問題かな？」
「まず何をそろえればいいかな？」

と考えることで、問題は落ち着いて見えるようになります。

これは、暗記に頼る数学から、自分で考える数学へと成長している証拠です。

周囲の大人にできるサポート

保護者や指導者にできることは、「正解かどうか」を見ることだけではありません。

「何を1にしたの？」
「どう考えたの？」

と問いかけることで、子どもの思考は深まります。

答えを急がせず、考え方を言葉にさせること。それが、算数・数学を得意科目へと変えていく最も確実なサポートです。

単位量当たりの大きさは、算数・数学全体を支える“背骨”のような考え方です。ここがしっかりしていれば、文章題も、速さも、割合も、中学数学も、一本の線でつながって見えるようになります。

算数・数学が苦手だと感じている子も、これから学ぶ子も、大切なのは「正しい順序で理解すること」。その第一歩として、単位量当たりの考え方を、ぜひじっくり身につけていってください。

―「単位量当たり」の理解が、算数・数学を変える ―

このコラムでは、小学校算数から中学校数学へとつながる「単位量当たりの考え方」について、さまざまな角度から解説してきました。

速さ・割合・平均という、一見すると別々に見える単元が、実はすべて同じ考え方で成り立っていること、そしてその理解があるかどうかで、中学数学での伸び方に大きな差が生まれることをお伝えしてきました。

算数が苦手になる子の多くは、「計算ができない」のではなく、

「何を1と考えているのか」
「1あたりとはどういう意味なのか」

があいまいなまま、式だけを追いかけてしまっています。

反対に、算数・数学が得意な子は、答えを出す前に

「これは何を比べている問題なのか」
「1つ分にするとどうなるか」

を自然と考えています。この差は、小学校高学年から少しずつ広がり、中学生になる頃には、文章題・関数・グラフの理解度としてはっきり表れてきます。

特に重要なのは、いきなり式を立てないことです。

言葉で説明し、図や表、線分図に表すことで、「考え方の流れ」を頭の中で整理する習慣が身につきます。この習慣こそが、応用問題や初見の問題に強くなる土台になります。学校のテストでは点が取れていても、少し形が変わった問題でつまずいてしまうのは、この土台が十分に育っていないことが原因である場合が少なくありません。

中学数学で学ぶ比例・反比例・関数、さらには「変化の割合」やグラフの傾きも、すべて「単位量当たりの大きさ」という考え方に行き着きます。ここを理解していれば、公式を丸暗記する必要はありません。

「なぜその式になるのか」
「この数値は何を表しているのか」

を自分で説明できるようになり、数学が“覚える教科”から“考える教科”へと変わっていきます。

もし今、算数や数学につまずいていたとしても、決して遅すぎることはありません。大切なのは、前に戻って「単位量当たり」という考え方を、丁寧に言葉と図で整理し直すことです。一つひとつ理解がつながった瞬間、これまでバラバラに見えていた問題が、驚くほどシンプルに感じられるようになります。

これから学ぶ子も、今まさにつまずいている子も、算数・数学が得意になる第一歩は同じです。

「1あたりで考える」
「言葉で説明する」
「図で整理する」

この3つを大切にしながら学習を続けていけば、必ず自信につながっていきます。算数・数学は、正しく理解すれば、誰にとっても“わかる”“おもしろい”教科です。焦らず、少しずつ、一緒に積み重ねていきましょう。

お子さまの学習にお悩みの保護者の方へ。

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。

→　無料の個別相談会の予約はコチラ　←

※一人ずつ個別で対応させていただいていますので、【事前予約制】となっています。

お気軽にどうぞ！！

こちら各種SNSでも情報配信中です。参考にしてみてください。

FACEBOOK

X（旧Twitter）

Instagram

この記事は 11人に閲覧されています。