速さの単位変換、なんとなくで解いていませんか？

このコラムでは、速さの基本から時速・分速・秒速の違い、単位変換のルールやコツまでを5つの章に分けてわかりやすく解説します。
「なるほど、そういうことか！」と納得できる内容を、ぜひ親子でご活用ください。

速さとは？

 

速さの学習は、算数や数学における「比」の考え方の第一歩です。速さとは、「1時間で何km進むか」「1秒で何m進むか」など、一定時間に進む距離のことを指します。ここで重要なのが基本公式です。

たとえば、120kmの道を2時間で走った場合の速さは「120 ÷ 2 = 60（km/h）」となります。

この式をしっかり覚えるために、「ハジキ」と呼ばれる図を使うのがおすすめです。

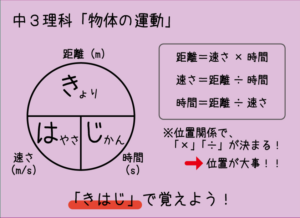
丸の中に「道のり/距離（上）」「速さ・時間（下）」を配置し、隠した部分を求めるようにすれば、速さ・道のり（距離）・時間の関係を直感的に理解できます。

また、速さの単位には以下のような種類があります：

• km/h（キロメートル毎時）

• m/s（メートル毎秒）

• m/min（メートル毎分）

これらの単位の違いが、次の章で扱う「単位変換」につながっていきます。速さの本質は変わらなくても、「時間」や「距離」の単位によって表し方が変わるため、まずは「速さ＝道のり÷時間」の考えをしっかり定着させることが大切です。

 

 

時速・分速・秒速の違いと単位変換のルール

 

 

速さには「時速（km/h）」「分速（m/min）」「秒速（m/s）」の3つの単位があります。これらはすべて「一定時間あたりに進む距離」を表していますが、時間の単位が違うだけで、数字の表し方や計算の仕方も変わってきます。

たとえば、時速60kmとは「1時間に60km進む速さ」、秒速5mとは「1秒間に5m進む速さ」です。この違いをきちんと理解しておかないと、単位を変えるときに混乱してしまいます。

ここで重要になるのが、単位変換のルールです。

• 時速（km/h）→ 分速（m/min）：×1,000 ÷ 60

• 分速（m/min）→ 秒速（m/s）：÷ 60

• 秒速（m/s）→ 時速（km/h）：× 3.6（暗記しておくと便利！）

たとえば、時速36km/hは「36 × 1,000 ÷ 60 = 600 m/min」、さらに「600 ÷ 60 = 10 m/s」と変換できます。逆に秒速から時速を求めるときは「秒速 × 3.6」で一発変換できます。

ここで混乱しやすいのが、「なぜ60で割ったりかけたりするのか？」という点です。これは「1時間＝60分」「1分＝60秒」という時間の単位の違いが原因で、速さの「時間」の部分を変えるために必要な操作です。

 

 

単位変換の具体例と計算練習

 

速さの単位変換は、知識として覚えるだけでなく、実際に計算してみることが重要です。ここでは、代表的な変換パターンを例に取り、実際の計算方法を確認していきましょう。

 

■　例1：時速を分速に変換

時速6km = 6,000m ÷ 60分 = 100m/分（分速）

ステップ１）　「kmをmに」＝ ×1,000

ステップ２）　「時間を分に」＝ ÷60

この順番で計算すればOKです。

■　例2：秒速から時速に変換

秒速5m = 5m × 60秒 × 60分 ÷ 1,000m = 18km/h

ステップ１）　「1秒あたりの距離 × 60」で1分の距離

ステップ２）　さらに ×60で1時間あたり

ステップ３）　最後に ÷1,000でm→kmへ

あるいは「秒速 × 3.6」で一気に変換してもOK！

 

■　例3：分速を秒速に変換

分速240m = 240 ÷ 60 = 4m/s

ステップ１）　「1分あたり」から「1秒あたり」なので、÷60

→　逆に秒速から分速なら ×60になります。

 

こうした変換の際に多いミスが、「÷60」と「×60」の方向を逆にしてしまうこと。「時間の単位が小さくなると数字は大きくなる」「大きくなると数字は小さくなる」と覚えておくと判断しやすくなります。また、1つの単位からいきなり別の単位に変えようとせず、途中の段階を踏んで変換していくことで、ミスを防げます（例：時速→分速→秒速と段階的に変換）。

速さの文章題に挑戦！問題文の読み解き方

 

速さの問題で一番ミスが出やすいのが、文章題の読み違いと単位のミスです。式を正しく立てられても、単位の違いに気づかず計算ミスになるケースが非常に多いです。

たとえば、「ある人が時速4kmで30分歩いた時の距離は？」という問題。

 

また、「何を求めるか」に応じて、使う公式も変わります。

• 距離を求める → 速さ × 時間

• 時間を求める → 距離 ÷ 速さ

• 速さを求める → 距離 ÷ 時間

この時、「道のり」「時間」「速さ」がそれぞれどの単位で出ているかを表や図で整理すると非常に分かりやすくなります。

 

文章題は、日本語の読解力と数学的な整理力の両方が問われます。慣れるまでは1問にじっくり時間をかけて、「読んで→図にして→式を立てる」練習を重ねることが大切です。

 

 

速さの学習を楽しくするための勉強法とコツ

「速さ＝道のり÷時間」のような公式は、暗記だけでは定着しにくいものです。だからこそ、視覚や体感を活かした勉強法が有効です。「ハジキ」の図をノートに何度も描いてみたり、表やグラフで「時間と距離の関係」を見える化することで、数字だけの世界がぐっと分かりやすくなります。

速さの学習は、単に計算力を鍛えるだけではなく、考える力や実生活への応用力も育てることができます。苦手意識を持たず、「どうしたら面白く学べるか」を意識することで、きっと速さが得意な単元へと変わっていくはずです。

速さの単位変換は「理解」と「体感」で得意になる！

今回のコラムを参考に、「理解できた！」「やってみようかな」という気持ちが一つでも芽生えたなら、それは大きな一歩です。
速さが苦手な単元から、得意な単元に変わるよう、ぜひ毎日の学習に役立ててください。

---

 

お子さまの学習にお悩みの保護者の方へ。

 

当塾では、一人ひとりの理解に合わせた“意味のある学び”を大切にした指導を行っています。「〇〇がニガテ」「家庭学習で何をすればいいかわからない」といったご相談も、お気軽にお寄せください。

まずは、無料体験授業で教え方の違い、学びの楽しさをご体感ください。

---

こちら各種SNSでも情報配信中です。参考にしてみてください。

 

 

/

この記事は 16人 に閲覧されています。